Lowest common denominator Facts for Kids

The lowest common denominator (also called the least common denominator or LCD) is a super helpful number in math! It's the smallest number that can be the bottom part (the denominator) of two or more fractions at the same time. Think of it as finding a common ground for fractions so you can easily add, subtract, or compare them.

What is the Lowest Common Denominator?
- Why is the LCD Important?
How to Find the LCD
- Step-by-Step Example
- Using the LCD to Rewrite Fractions
LCD with Variables
See also

What is the Lowest Common Denominator?

The lowest common denominator, or LCD, is like a special helper for fractions. When you have fractions with different denominators, it's hard to work with them. For example, you can't easily add 1/2 and 1/3 directly. The LCD helps you change these fractions into new ones that have the same bottom number. This makes math much simpler!

Why is the LCD Important?

The LCD is important for a few key reasons:

Adding and Subtracting: You can only add or subtract fractions if they have the same denominator. The LCD helps you find that common denominator.
Comparing Fractions: It's much easier to see which fraction is bigger or smaller when they share the same denominator.
Solving Problems: Many math problems involving fractions become much clearer once you find the LCD.

How to Find the LCD

Finding the LCD is like finding the least common multiple (LCM) of the denominators. The LCM is the smallest number that is a multiple of all the numbers you are looking at.

Step-by-Step Example

Let's find the LCD for the fractions $\frac{1}{2}$ and $\frac{2}{3}$ .

Step 1: Look at the denominators.

The denominators are 2 and 3.

Step 2: List multiples of each denominator.

Multiples of 2 are: 2, 4, 6, 8, 10, 12... Multiples of 3 are: 3, 6, 9, 12, 15...

Step 3: Find the smallest common multiple.

The smallest number that appears in both lists is 6. So, the LCD of 2 and 3 is 6.

Using the LCD to Rewrite Fractions

Once you find the LCD, you can rewrite your original fractions so they have this new common denominator.

For $\frac{1}{2}$ : To change the denominator from 2 to 6, you multiply 2 by 3. You must do the same to the top number (numerator).

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{1}{2} \cdot \frac{3}{3} = \frac{3}{6}

For $\frac{2}{3}$ : To change the denominator from 3 to 6, you multiply 3 by 2. You must do the same to the top number.

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{2}{3} \cdot \frac{2}{2} = \frac{4}{6}

Now, $\frac{1}{2}$ becomes $\frac{3}{6}$ and $\frac{2}{3}$ becomes $\frac{4}{6}$ . They both have the same denominator, 6! This makes it easy to add them: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{3}{6} + \frac{4}{6} = \frac{7}{6} .

LCD with Variables

The idea of the LCD also works when your denominators include variables, like 'x'. You still look for the smallest expression that all denominators can divide into evenly.

For example, let's look at Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{1}{2x} + \frac{3}{x^2} .

The denominators are 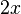$2x$ and $x^2$ .
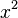The LCD for these two is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2x^2 .
To change Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{1}{2x} to have Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2x^2 as its denominator, you multiply the top and bottom by $x$ :

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{1}{2x} \cdot \frac{x}{x} = \frac{x}{2x^2}

To change Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{3}{x^2} to have Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2x^2 as its denominator, you multiply the top and bottom by $2$ :

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{3}{x^2} \cdot \frac{2}{2} = \frac{6}{2x^2}

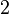Now you can add them:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{x}{2x^2} + \frac{6}{2x^2} = \frac{x+6}{2x^2}

Lowest common denominator facts for kids

Contents