Missing square puzzle facts for kids
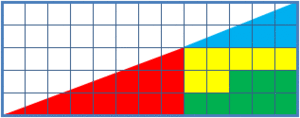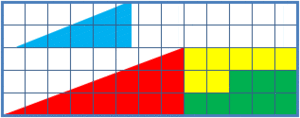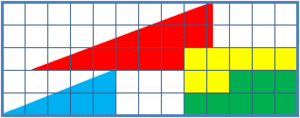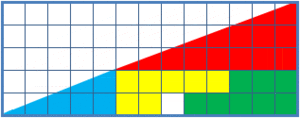
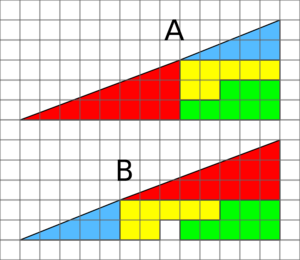
The missing square puzzle is a cool optical illusion often used in math classes. It helps students learn to think carefully about shapes and not just trust what their eyes see! The puzzle shows two arrangements of the same shapes. Each one looks like a big triangle, 13 units wide and 5 units tall. But here's the trick: one of the arrangements has a small 1x1 hole, or "missing" square, in it!
How the Puzzle Works
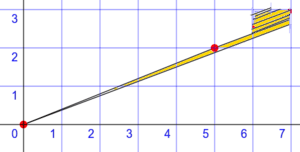
The secret to this puzzle is that neither of the big 13x5 "triangles" is actually a perfect triangle. What looks like the long, sloped side (called the hypotenuse) is actually bent! It's not a straight line, even though it looks like one. This means the slope of that line changes slightly.
A real 13x5 triangle can't be made from these specific pieces. The four shapes (yellow, red, blue, and green) add up to 32 square units of area. If the big shape were a true 13x5 triangle, its area should be (13 × 5) / 2 = 32.5 square units.
But look closely:
- The blue triangle has a side ratio of 5:2 (which is 2.5).
- The red triangle has a side ratio of 8:3 (which is about 2.667).
Because these ratios are different, the "hypotenuse" of the combined shape is actually bent.
- The first arrangement of shapes covers exactly 32 square units.
- The second arrangement covers 33 square units, which includes the "missing" square!
The bend is super tiny, about 1/28th of a unit. It's really hard to spot! If you look at the grid point where the red and blue triangles meet in the lower image (5 squares right, 2 squares up), you'll see the line goes through it. But in the upper image, the line is slightly below that point. If you put the "hypotenuses" from both figures on top of each other, they form a very thin, flat shape called a parallelogram. This thin parallelogram has an area of exactly one grid square – that's your "missing" area!
Who Invented It?
This specific puzzle was created by an amateur magician named Paul Curry in New York City in 1953. But the idea of puzzles where shapes seem to gain or lose area has been around since the 1500s!
The sizes of the pieces in this puzzle (2, 3, 5, 8, 13) are special numbers. They are all Fibonacci numbers! Fibonacci numbers are a sequence where each number is the sum of the two before it (like 1, 1, 2, 3, 5, 8, 13...). Using these numbers helps create that perfect one-unit "missing" area. Many other cool shape puzzles use properties of the Fibonacci sequence.
Similar Puzzles
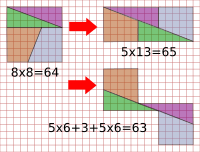
Sam Loyd's chessboard paradox is another puzzle like this. It shows how an 8x8 square can be rearranged into a 5x13 rectangle. In the rectangle, the small gaps between the pieces add up to one extra square unit of area. This makes it look like the pieces take up more space than they did in the original square!
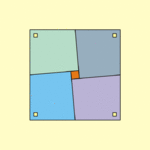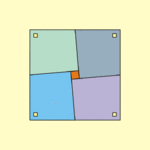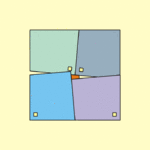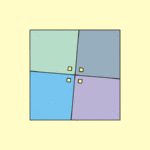
Mitsunobu Matsuyama also created a "paradox" using four shapes with four sides (quadrilaterals) and a small square. They form a larger square. When you spin the quadrilaterals, they seem to fill the space of the small square, but the total area of the big shape looks the same. The trick here is that the side of the new large square is actually a tiny bit smaller than the original one!
See also
 In Spanish: Paradoja del cuadrado perdido para niños
In Spanish: Paradoja del cuadrado perdido para niños