Morwen Thistlethwaite facts for kids
Quick facts for kids
Morwen Thistlethwaite
|
|
|---|---|
| Born |
Morwen Bernard Thistlethwaite
5 June 1945 |
| Nationality | British |
| Alma mater | University of Manchester PhD University of London (MSc.) University of Cambridge (BA) |
| Spouse(s) | Stella Thistlethwaite |
| Scientific career | |
| Fields | Mathematics |
| Institutions | University of Tennessee |
| Doctoral advisor | Michael George Barratt |
Morwen Bernard Thistlethwaite, born on June 5, 1945, is a British mathematician. He is known for his work in knot theory, which studies how knots are formed and behave. He is also a professor of mathematics at the University of Tennessee in Knoxville. Thistlethwaite has made big contributions to both knot theory and the math behind the Rubik's Cube.
Contents
About Morwen Thistlethwaite
Morwen Thistlethwaite earned his first degree, a Bachelor of Arts (BA), from the University of Cambridge in 1967. He then received his Master of Science (MSc) from the University of London in 1968. In 1972, he completed his PhD at the University of Manchester.
Before focusing on math, Thistlethwaite studied piano. He even gave concerts in London. In 1975, he decided to pursue a career in mathematics. He taught at two different polytechnic schools in London until 1987.
After that, he was a visiting professor at the University of California, Santa Barbara for one year. Later, he joined the University of Tennessee, where he is now a professor. His wife, Stella Thistlethwaite, also teaches at the University of Tennessee. His son, Oliver, is also a mathematician.
Thistlethwaite's Mathematical Work
Solving Knot Puzzles: Tait Conjectures
Morwen Thistlethwaite helped prove the Tait conjectures. These were three important ideas about knots. They helped mathematicians understand how knots are drawn and how they relate to each other.
Here are the three conjectures:
- The simplest drawings of certain knots (called alternating diagrams) have the fewest possible crossings.
- Any two simple drawings of the same knot have the same "writhe." This is a way to measure how much the knot twists.
- Any two simple drawings of a specific type of knot can be changed into each other using special moves called flypes.
Thistlethwaite, along with Louis Kauffman and Kunio Murasugi, proved the first two conjectures in 1987. He then worked with William Menasco to prove the third one, known as the Tait flyping conjecture, in 1991.
Rubik's Cube Solution: Thistlethwaite's Algorithm
Thistlethwaite also created a famous way to solve the Rubik's Cube. This method, called Thistlethwaite's algorithm, breaks down the solving process into steps. It restricts the cube's positions into smaller groups that are easier to solve.
The algorithm uses a series of groups, where each group has fewer possible moves:
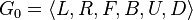 : This group includes all possible scrambled positions of the Rubik's Cube. You can use any turn (Left, Right, Front, Back, Up, Down).
: This group includes all possible scrambled positions of the Rubik's Cube. You can use any turn (Left, Right, Front, Back, Up, Down).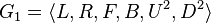 : In this group, you can only use quarter turns on the left, right, front, and back sides. But you can only use double turns on the up and down sides.
: In this group, you can only use quarter turns on the left, right, front, and back sides. But you can only use double turns on the up and down sides.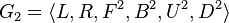 : Here, you can only use double turns on the front, back, up, and down faces. You can still use quarter turns on the left and right faces.
: Here, you can only use double turns on the front, back, up, and down faces. You can still use quarter turns on the left and right faces.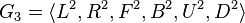 : For this group, you can only use double turns on all sides of the cube.
: For this group, you can only use double turns on all sides of the cube.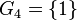 : This is the final group, which means the cube is completely solved!
: This is the final group, which means the cube is completely solved!
To solve the cube, you move from one group to the next. You use specific moves to get the cube into the next, simpler group. You keep doing this until the cube is solved.
Naming Knots: Dowker–Thistlethwaite Notation
Thistlethwaite, working with Clifford Hugh Dowker, created a special way to write down knots. It's called Dowker–Thistlethwaite notation. This system is very useful for computers to understand and work with different knots. It was based on older ways of describing knots by mathematicians like Peter Guthrie Tait and Carl Friedrich Gauss.
Awards and Recognition
In 2022, Morwen Thistlethwaite was named a Fellow of the American Mathematical Society. This honor recognized his important work in a field called low-dimensional topology. Specifically, he was honored for solving the classical knot theory puzzles by Tait and for helping to list and organize different knots.
See also


