Noether's theorem facts for kids

Noether's theorem is a very important idea in physics. It says that for every continuous symmetry a physical system has, there is a quantity that stays the same, or is "conserved." This means the quantity doesn't change over time.
A "symmetry" here means that something looks or behaves the same even after you change it in some way. For example, if a physics experiment works the same way no matter where you do it, that's a symmetry of space.
The theorem was proven by a brilliant mathematician named Emmy Noether in 1915. It helps us understand why many things in the universe, like energy and momentum, are conserved. This theorem applies to symmetries that are smooth and continuous, like moving something a little bit or rotating it slightly.
Noether's theorem is used a lot in theoretical physics. It helps scientists find out what quantities are conserved in different systems.
Contents
What is a Symmetry in Physics?
A "symmetry" in physics means that a system or its laws of motion look the same even after you do something to them. Imagine a perfectly round ball. If you spin it, it still looks the same. That's a symmetry!
Noether's theorem connects these symmetries to "conservation laws." A conservation law means that a certain quantity, like energy or momentum, always stays the same in a system. It doesn't get lost or gained.
How Does Symmetry Lead to Conservation?
Let's look at some examples to make this clearer:
- Moving in Space: If the laws of physics work the same no matter where you are, then the system has a symmetry of "translation" (moving from one place to another). Noether's theorem says this means momentum is conserved. Momentum is how much "oomph" something has when it moves.
- Spinning Around: If a system behaves the same no matter how it's turned or oriented in space, it has a "rotational" symmetry. From this, Noether's theorem tells us that angular momentum is conserved. Angular momentum is like the "oomph" of something spinning or orbiting. Even a tumbling, uneven asteroid conserves its angular momentum because the laws of motion are symmetric.
- Time Passing: If a physical process works the same today as it did yesterday, it has a "time translation" symmetry. This symmetry means that energy is conserved. Energy is the ability to do work.
Noether's theorem is super important. It helps scientists figure out what quantities will be conserved just by looking at the symmetries of a system. It also helps them create new theories by thinking about what quantities they want to be conserved.
Noether's Theorem in Simple Words
Emmy Noether's big idea can be put simply:
If a system has a continuous symmetry, then there are quantities that stay the same over time.
Think of it like this: If you can change something about a system (like its position or direction) and it still behaves exactly the same way, then there's a special number or value connected to that change that will always stay constant.
This "symmetry" is about how the rules of physics work. It's not about the object itself. For example, a spinning, wobbly top might not look perfectly symmetric, but the laws that govern its spin are symmetric. This means its angular momentum is conserved.
The conserved quantity is often called the "Noether charge," and its flow is called the "Noether current." Imagine water flowing through pipes; the current is the flow, and the charge is the amount of water. If the total flow into a section of pipe equals the total flow out, the amount of water inside that section is conserved.
A Quick Look at the Idea
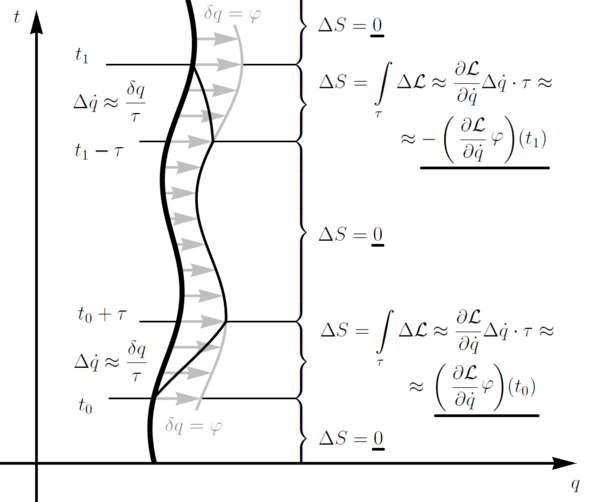
Let's imagine a simple system that moves along a path. If this system has a continuous symmetry, it means you can slightly change its path in a specific way, and the "action" (a special value that describes the path) won't change.
Noether found that if the action doesn't change under a small, continuous symmetry, then a certain quantity related to the system must be conserved. This quantity's value will be the same at the beginning and end of any time period.
For example, if the symmetry is just moving the system a little bit (a "translation"), then the conserved quantity turns out to be its momentum.
This idea extends to more complex systems, like fields (which are values spread out over space, like temperature or electric fields). In those cases, instead of a single conserved quantity, you get a "conserved current." This current describes how the conserved quantity flows through space and time. If the total flow of this current into a region equals the total flow out, then the amount of the conserved quantity inside that region stays the same.
How We Discovered Conservation Laws
For a long time, scientists noticed that certain things seemed to stay constant in nature. These are called conservation laws.
- Early Ideas: In the 1600s, thinkers like René Descartes and Gottfried Leibniz noticed that momentum and a form of energy (kinetic energy) seemed to be conserved during collisions.
- Newton's Laws: Isaac Newton later showed that the conservation of momentum was a direct result of his third law of motion (for every action, there is an equal and opposite reaction).
- Lagrangian Mechanics: In the late 1700s, a new way to describe motion, called Lagrangian mechanics, was developed. It uses a special function called the Lagrangian. If a certain "coordinate" (a way to describe the system's position) doesn't appear in the Lagrangian, it means the system is symmetric with respect to that coordinate. This directly leads to a conserved quantity, often momentum. This was a hint of Noether's bigger idea.
Noether's theorem took these separate observations and showed a deep, underlying reason for all of them: symmetry.
Examples of Noether's Theorem in Action
Noether's theorem helps us understand why fundamental laws of physics exist. Here are some key examples:
Conserving Energy
Imagine a simple object moving, like a ball rolling down a hill. Its energy is made of its kinetic energy (energy of motion) and potential energy (stored energy from its position).
If the laws governing the ball's motion don't change over time (meaning the Lagrangian doesn't depend on time), then Noether's theorem tells us that the total energy of the ball is conserved. It might change from potential to kinetic, but the total amount stays the same.
Conserving Momentum
If the laws of physics are the same no matter where you are in space (meaning the Lagrangian doesn't change if you shift the system's position), then Noether's theorem says that the system's linear momentum is conserved. This is why when two billiard balls hit each other, the total momentum before the collision is the same as after.
Conserving Angular Momentum
If the laws of physics are the same no matter how you rotate a system (meaning the Lagrangian doesn't change if you spin the system), then Noether's theorem tells us that the system's angular momentum is conserved. This is why a spinning ice skater speeds up when she pulls her arms in – her angular momentum must stay the same.
Applications of Noether's Theorem
Noether's theorem is a powerful tool for physicists. It allows them to understand the fundamental rules of the universe just by looking at symmetries.
- Space Translation: If physics works the same everywhere, then momentum is conserved.
- Rotation: If physics works the same no matter how you turn things, then angular momentum is conserved.
- Time Translation: If physics works the same yesterday, today, and tomorrow, then energy is conserved.
In more advanced physics, like quantum field theory, Noether's theorem also explains why electric charge is conserved. This comes from a symmetry related to how charged particles interact with electric and magnetic fields.
Noether's theorem shows us the deep and beautiful connection between symmetries in nature and the quantities that remain constant in our universe.
Images for kids
See also
 In Spanish: Teorema de Noether para niños
In Spanish: Teorema de Noether para niños