Position (geometry) facts for kids
A position vector is like a special arrow that points from a starting spot (called the origin) to a specific point in space. Imagine you're standing at the center of a room (your origin). If you want to tell someone where a toy is, you could point to it and say how far away it is. That pointing arrow is like a position vector!
In math, we often use letters like x, r, or s to show a position vector. It's basically a straight line from the origin to the point you're interested in. It tells you how far and in what direction something is from a known starting point.
Position vectors are super useful in subjects like mechanics (how things move) and geometry (the study of shapes and spaces). They help scientists and engineers describe where things are in two-dimensional (like a flat map) or three-dimensional space (like the world around us). They can even be used for more dimensions, but 2D and 3D are the most common.
Contents
Relative Position: Where is it Compared to That?
Sometimes, you don't want to know where something is from the main origin, but where it is compared to *another* point. This is called relative position.
Imagine you have two friends, Alex and Ben. You know where Alex is from your house (the origin). You also know where Ben is from your house. If you want to know where Ben is *from Alex's spot*, you're looking for their relative position.
You find the relative position by subtracting the position vector of the first point from the position vector of the second point. It's like drawing an arrow directly from the first point to the second point.
The relative direction is just that relative position arrow, but made into a "unit vector." A unit vector is a special vector that only tells you the direction, not the distance. It's like saying "that way!" without saying "that way for 5 meters."
Defining Position in Space
Using Coordinates
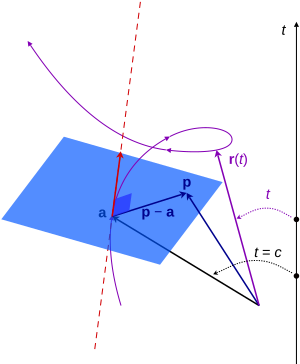
To describe where a point is in three dimensions, we use different ways of measuring, called coordinate systems. The most common one you might know is the Cartesian coordinate system, which uses `x`, `y`, and `z` values. Think of it like giving directions: "Go 5 steps forward (x), 3 steps right (y), and 2 steps up (z)."
Other ways to describe a position include:
- Spherical coordinates: These use a distance from the origin and two angles. Imagine telling someone where a star is: "It's 100 light-years away, at this angle up from the horizon, and this angle around from north."
- Cylindrical coordinates: These use a distance from a central line, an angle around that line, and a height. Think of finding a spot on a can: "It's this far from the center, at this angle around the can, and this high up."
No matter which system you use, they all describe the same exact spot in space. We pick the one that makes the math easiest for what we're trying to do!
How Position Vectors are Used
In Mechanics (How Things Move)
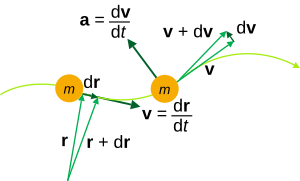
In mechanics, which is the study of how things move, the position vector is super important! If you know how the position vector of an object changes over time, you can figure out its entire journey. For example, if you know the position vector of a ball thrown in the air at every second, you can draw its path.
We often write the position vector as r(t), where `t` stands for time. This means the position of the object changes as time goes by.
What Happens When Position Changes?
When a position vector changes over time, we can calculate other important things about the object's motion:
- Velocity: This tells you how fast an object is moving and in what direction. It's found by looking at how the position vector changes over a very tiny amount of time.
* Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathbf{v} = \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}
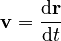
- Acceleration: This tells you how much an object's velocity is changing (speeding up, slowing down, or changing direction). It's found by looking at how the velocity vector changes over time.
* 
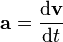
- Jerk: This is how much the acceleration is changing. It's less common in everyday talk, but important in some areas of physics and engineering.
* Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathbf{j} = \frac{\mathrm{d}\mathbf{a}}{\mathrm{d}t}
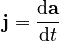
These ideas help us understand and predict the movement of everything from planets to cars!
See also
In Spanish: Posición para niños
- Coordinate system
- Horizontal position
- Vertical position
