Positive-definite matrix Facts for Kids

A positive-definite matrix is a special kind of matrix. Think of a matrix as a grid or table of numbers. Positive-definite matrices have unique properties that make them useful in many areas of mathematics and science. They are easiest to understand when they are square (meaning they have the same number of rows and columns) and symmetrical.

What is a Positive-Definite Matrix?

A matrix is called "positive-definite" if, when you do a specific calculation with it, the result is always a positive number. This calculation involves multiplying the matrix by a special kind of number list called a vector.

Imagine you have a square matrix, which is like a grid of numbers. For this matrix to be positive-definite, it must follow a rule:

You pick any vector (a list of numbers) that is not all zeros.
You perform a special multiplication: the vector's "transpose" (which means turning its rows into columns) times the matrix, and then times the original vector.
If the answer to this multiplication is always a positive number (greater than zero), no matter which non-zero vector you pick, then the matrix is positive-definite.

This property is very important in fields like engineering, physics, and computer science.

An Example of a Positive-Definite Matrix

Let's look at a simple example. The matrix below is a positive-definite matrix: 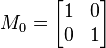$M_0 = \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix}$

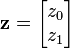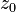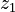This matrix is called an "identity matrix." To see why it's positive-definite, let's pick a vector, say $\textbf{z}= \begin{bmatrix} z_0 \\ z_1\end{bmatrix}$ . Here, $z_0$ and $z_1$ are just numbers.

When we do the special multiplication (vector transpose times matrix times vector), we get: 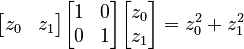$\begin{bmatrix} z_0 & z_1\end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} z_0 \\ z_1\end{bmatrix}=z_0^2+z_1^2$

The result is 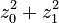$z_0^2+z_1^2$ .

If 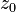$z_0$ is 3 and 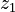$z_1$ is 4, then 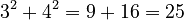$3^2 + 4^2 = 9 + 16 = 25$ , which is positive.
If 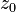$z_0$ is -2 and 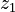$z_1$ is 1, then 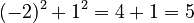$(-2)^2 + 1^2 = 4 + 1 = 5$ , which is also positive.

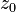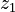As long as at least one of $z_0$ or $z_1$ is not zero, the sum of their squares ( 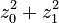$z_0^2+z_1^2$ ) will always be a positive number. This shows that the matrix 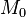$M_0$ is indeed positive-definite.

All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:

Positive-definite matrix Facts for Kids. Kiddle Encyclopedia.

Positive-definite matrix facts for kids

What is a Positive-Definite Matrix?

An Example of a Positive-Definite Matrix