Spirograph facts for kids
_(perspective_fixed).jpg)
Spirograph set (early 1980s UK version)
|
|
| Inventor(s) | Denys Fisher |
|---|---|
| Company | Hasbro |
| Country | United Kingdom |
| Availability | 1965–present |
| Materials | Plastic |
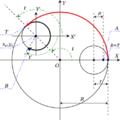
Spirograph is a cool drawing toy that helps you create amazing geometric patterns. These patterns are special mathematical curves called hypotrochoids and epitrochoids. The popular toy version was invented by a British engineer named Denys Fisher. It was first sold in 1965.
The name Spirograph is a registered trademark of Hasbro Inc. Hasbro bought the company that owned Denys Fisher's original company in 1998. In 2013, the Spirograph brand was brought back worldwide by Kahootz Toys, with its classic toy sets.
How to Use a Spirograph
The first Spirograph sets came with two plastic rings. These rings had gear teeth on both their inside and outside edges. You would hold one of these rings still, maybe with pins, tape, or just your hand.
Then, you would pick one of the smaller gearwheels. These gearwheels have small holes where you put a ballpoint pen. You would spin this gearwheel around the fixed ring. As you spin it, the pen draws a beautiful geometric shape!
Later versions, like the Super-Spirograph, added more shapes. These included extra rings, triangles, and even straight bars. All the pieces have teeth that fit together. Smaller gears can roll inside the larger rings, or even roll along their outside edge. You can also make gears roll around each other!
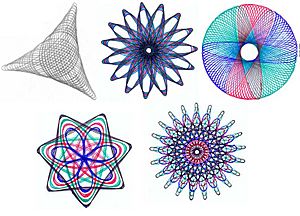
You can combine the gears in many different ways to make unique designs. Many sets also came with pens in different colors. Switching colors while you draw can make your designs even more awesome, as you can see in the pictures.
When you're just starting, the gears might slip sometimes. This can happen especially when you use the holes near the edge of the bigger wheels. This might make your lines broken or uneven. But with practice, you'll get better! Experienced users can even learn to move several pieces at once to create even more complex patterns.
Images for kids
-
A mathematical drawing that shows how Spirograph patterns are made.
See also
In Spanish: Espirógrafo para niños
