Tensor product of graphs facts for kids

The tensor product of graphs.

In graph theory, a graph is like a map with dots (called vertices or nodes) and lines connecting them (called edges). The tensor product of two graphs, let's call them G and H, is a way to combine them into a brand new, larger graph.

Imagine you have two simple graphs. When you make their tensor product, the new graph will have many more vertices and edges. It's like mixing two different sets of ingredients to create a new dish!

What is the Tensor Product?

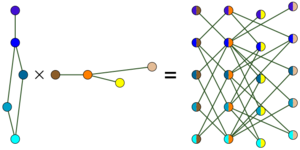
The tensor product of graphs G and H is written as G × H. Here's how it works:

• New Vertices: The new graph G × H has vertices that are pairs of vertices from the original graphs. If G has vertices {1, 2} and H has vertices {A, B}, then G × H will have vertices like (1, A), (1, B), (2, A), and (2, B). This is called a Cartesian product.
• New Edges: An edge exists between two new vertices, say (g,h) and (g,h), only if:

* g is connected to g' in graph G, AND * h is connected to h' in graph H.

Both conditions must be true for an edge to exist in the new graph.

Other Names for the Tensor Product

The tensor product has many other names! People also call it the:

• Direct product
• Kronecker product
• Categorical product
• Cardinal product
• Relational product
• Weak direct product
• Conjunction

This idea of combining things was first introduced by famous thinkers Alfred North Whitehead and Bertrand Russell in their book Principia Mathematica in 1912.

You might also hear about the Kronecker product of matrices. The tensor product of graphs is related to this, as it's like combining the "connection maps" (called adjacency matrices) of the two graphs.

It's important not to confuse the tensor product with other ways of combining graphs, like the Cartesian product of graphs or the strong product of graphs. Even though the symbol '×' is used for both tensor and Cartesian products, they create very different results!

Examples of Tensor Products

Let's look at some cool examples:

• If you take any graph G and combine it with a graph that has just two vertices connected by an edge (called K₂), you get a special graph called a bipartite graph. This new graph is known as the bipartite double cover of G.
• For instance, if you take the Petersen graph and combine it with K₂, you get the Desargues graph.
• Imagine a complete graph (where every vertex is connected to every other vertex). If you take its tensor product with itself, you get a graph that looks like a Rook's graph but with all its connections flipped (this is called the complement). You can imagine its vertices arranged in a grid, where each vertex is connected to all others not in its row or column.

Properties of the Tensor Product

The tensor product has some interesting features:

• Connectivity: The new graph G × H will be connected (meaning you can get from any vertex to any other vertex) only if both original graphs G and H are connected, AND at least one of them is not bipartite. A bipartite graph is one whose vertices can be divided into two groups, and all edges connect a vertex from one group to a vertex in the other.
• Bipartite Result: If either of the original graphs G or H is bipartite, then their tensor product G × H will also be bipartite.

Scientists have studied the tensor product for a long time. For example, there was a famous idea called the Hedetniemi conjecture about the "coloring" of tensor product graphs. However, this idea was shown to be incorrect in 2019.

See also

• Graph product
• Strong product of graphs