The monkey and the coconuts facts for kids
The monkey and the coconuts is a famous mathematical puzzle. It's about five sailors and a monkey on a desert island who find a big pile of coconuts. The puzzle asks you to figure out how many coconuts were in the pile to start with. You can't have parts of coconuts, only whole ones! This puzzle is known for being tricky, but there are clever math ways to solve it. It's a popular problem in books and games about math.
Contents
What is the Puzzle About?
Here's how the puzzle usually goes:
- There's a pile of coconuts. Five men own them.
- One man wakes up in the night. He divides the coconuts into five equal piles. There's one coconut left over, so he gives it to a monkey. He takes his share and hides it. Then he puts the rest of the coconuts back together.
- Later, a second man wakes up and does the exact same thing. He divides the remaining coconuts into five piles, gives one leftover coconut to the monkey, takes his share, and puts the rest back.
- The third, fourth, and fifth men all do the same thing. Each time, there's one coconut left over for the monkey.
- The next morning, all five men wake up. They divide the coconuts that are left into five equal piles. This time, there are NO coconuts left over.
- The big question is: How many coconuts were in the original pile at the very beginning?
This puzzle is a great example of "monkey and coconut type problems." These are math puzzles where you have to find whole number answers after dividing things many times, sometimes with leftovers.
The Puzzle's History
Puzzles like this have been around for a very long time! Some similar problems were found in ancient Indian math books from about 850 CE. Even older Chinese writings from the first century CE had puzzles about finding numbers based on leftovers after division.
The famous writer Lewis Carroll (who wrote "Alice in Wonderland") wrote down a similar puzzle in his diary in 1888. His version was about four brothers and a pile of nuts, with one nut left for a monkey each time.
The "monkey and the coconuts" puzzle became super famous when an American writer named Ben Ames Williams included it in his short story "Coconuts." This story was published in a popular magazine called The Saturday Evening Post on October 9, 1926.
Here's how Williams described the puzzle in his story: Five men and a monkey were shipwrecked. They gathered coconuts. That night, one man woke up and secretly divided the coconuts into five piles. One coconut was left, so he gave it to the monkey. He hid his share, put the rest back, and went to sleep. The second, third, fourth, and fifth men did the same thing. Each time, one coconut was left for the monkey. The next morning, they all divided the remaining coconuts into five equal shares, and this time, there were no coconuts left over. How many coconuts were there at the start?
Williams didn't include the answer in his story! The magazine was flooded with over 2,000 letters from readers begging for the solution. The editor even sent Williams a telegram saying, "FOR THE LOVE OF MIKE, HOW MANY COCONUTS? HELL POPPING AROUND HERE." Williams kept getting letters about the puzzle for twenty years!
Martin Gardner, a famous writer about math puzzles, wrote about this problem in 1958. He said it was one of his favorite puzzles because it was so tricky. The version Williams used, where the final division has no leftovers, is the most popular one today.
How to Solve It
Solving this puzzle by just guessing numbers would take a very long time! The smallest positive answer is quite large. Mathematicians use special methods to find the solution.
The Idea of "Negative Coconuts"
One clever way to think about the original puzzle (where there's one coconut left over even in the morning) is to imagine "negative coconuts." It sounds silly, but it helps with the math! If you start with -4 coconuts, the puzzle works out perfectly with negative numbers. Then, you can add a certain number of coconuts (15,625 in this case) to get the smallest positive answer. For the original puzzle, the answer is 15,621 coconuts.
The "Blue Coconuts" Trick
Another helpful trick, especially for Williams's version, is to imagine adding some "blue coconuts" to the pile at the very beginning. Let's say you add four imaginary blue coconuts. Now, the pile is perfectly divisible by five, with no remainder. Each sailor takes their share, and the blue coconuts are set aside. After all the divisions, you just subtract the blue coconuts you added.
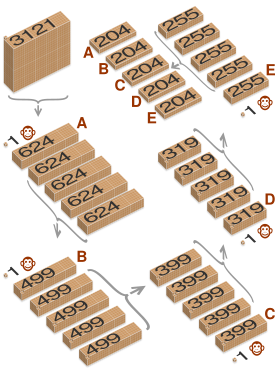
Since there are five sailors, and each time they divide by five, the original pile (plus the blue coconuts) must have been a multiple of 5 multiplied by itself five times (5x5x5x5x5 = 3125). So, if you started with 3125 coconuts (including the blue ones), and then subtract the 4 blue coconuts, you get 3121. This is the smallest number of coconuts for Williams's version!
Using Patterns (Base 5)
Mathematicians can also solve this puzzle by looking at patterns in a special number system called "base 5." In our everyday counting, we use "base 10" (numbers 0-9). But if you count in "base 5" (using only 0-4), the way the coconuts are divided and taken away creates a clear pattern. When you write the answer in base 5, it looks like 44441. If you change that back to our normal base 10 numbers, you get 3121.
The Answer
For the version of the puzzle made famous by Ben Ames Williams, where the final division in the morning has no coconuts left over, the smallest number of coconuts in the original pile is 3121.
After the five sailors each take their share and give one to the monkey, there are 1020 coconuts left in the morning. When they divide 1020 by 5, each sailor gets 204 coconuts, with no leftovers.
Mathematicians use advanced tools like Diophantine equations and the Euclidean algorithm to find these solutions. These methods help them find whole number answers to equations that have many possible solutions.