Adder (electronics) Facts for Kids

An adder is a special digital circuit that helps computers add numbers. Think of it as the calculator part inside a computer's brain! Adders are super important in the arithmetic logic units (ALUs) of processors. These ALUs are like the math teachers of a computer, handling all the calculations. Adders also help with other tasks, like figuring out where information is stored in memory or counting things.

While adders can work with different ways of representing numbers, they usually work with binary numbers. Binary numbers use only 0s and 1s, which is how computers understand information. If a computer uses a special way to show negative numbers (like two's complement), it's easy to change an adder into a circuit that can both add and subtract.

History
Binary Adders
Images for kids
See also

History

In 1937, a smart person named Claude Shannon showed how to add binary numbers using circuits in his project at MIT. This was a big step for computers!

Binary Adders

Computers use special circuits to add binary numbers. Let's look at the basic types.

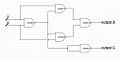
Half Adder

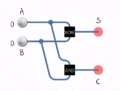
A half adder is the simplest kind of adder. It adds two single binary digits, let's call them A and B. It has two outputs:

Sum (S): This is the result of the addition.
Carry (C): This signal tells us if there's an "overflow" into the next place value, just like when you carry a 1 in regular addition (e.g., 5 + 5 = 10, you write 0 and carry 1).

The simplest way to build a half adder uses two basic logic gates:

An XOR gate for the Sum (S).
An AND gate for the Carry (C).

Here's how a half adder works with different inputs:

Inputs		Outputs
A	B	C_out	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

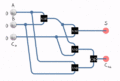
Full Adder

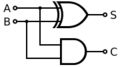
A full adder is more advanced than a half adder. It can add three single binary numbers:

A and B: These are the two numbers you want to add.
C_in: This is a "carry-in" bit from an earlier, less important addition stage.

A full adder is often used as a building block for adding larger binary numbers (like 8-bit, 16-bit, or 32-bit numbers). It produces two outputs:

Sum (S): The result of the addition.
C_out: The "carry-out" bit, which goes to the next addition stage.

You can build a full adder using two half adders and one OR gate.

The first half adder takes A and B as inputs.
Its sum output goes into the second half adder, along with C_in.
The carry outputs from both half adders are combined using an OR gate to create the final C_out.

Here's how a full adder works with different inputs:

Inputs			Outputs
A	B	C_in	C_out	S
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

Adders Supporting Multiple Bits

To add numbers with many binary digits (like 8-bit or 32-bit numbers), we connect several full adders together.

Ripple-Carry Adder

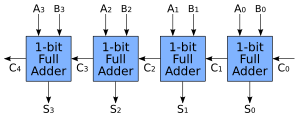
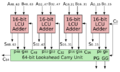
A 4-bit ripple-carry adder.

A ripple-carry adder (RCA) is made by linking many full adders in a chain. The "carry-out" (C_out) from one full adder becomes the "carry-in" (C_in) for the next one. This is like how you carry a number to the next column when doing addition by hand.

The design of a ripple-carry adder is simple to understand. However, it can be a bit slow. Each full adder has to wait for the carry bit from the one before it. This "rippling" of the carry bit takes time, especially for very long numbers.

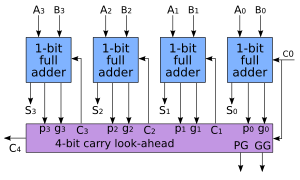
Carry-Lookahead Adder

A 4-bit adder that uses carry lookahead.

To make addition faster, engineers invented carry-lookahead adders (CLA). Instead of waiting for the carry to ripple, these adders try to figure out the carry bits much faster. They do this by looking ahead at the inputs to predict the carries. This allows all the carry bits to be calculated at almost the same time, which speeds up the whole addition process.

There are also other ways to design multi-bit adders, like the carry-skip adder and the carry-select adder. These designs also aim to make the addition process quicker by optimizing how carry bits are handled.

Images for kids

Half adder in action.
Schematic of half adder implemented with one XOR gate and one AND gate.
Schematic of half adder implemented with five NAND gates.
Schematic symbol for a 1-bit half adder.
Full adder in action.
Schematic of full adder implemented with two XOR gates, two AND gates, one OR gate.
Schematic of full adder implemented with nine NAND gates.
Schematic of full adder implemented with nine NOR gates.
Full adder with inverted outputs with single-transistor carry propagation delay in CMOS
Schematic symbol for a 1-bit full adder with C_in and C_out drawn on sides of block to emphasize their use in a multi-bit adder
Decimal 4-digit ripple carry adder. FA = full adder, HA = half adder.
64-bit adder with carry lookahead

Adder (electronics) facts for kids

Contents