Carlyle circle facts for kids

A Carlyle circle is a special type of circle used in mathematics. It helps us find the answers (called "solutions" or "roots") to certain math problems called quadratic equations. Imagine a graph with an X-axis (horizontal line) and a Y-axis (vertical line). When you draw a Carlyle circle, the points where it crosses the X-axis are exactly the solutions to the quadratic equation it's linked to!

This clever circle is named after Thomas Carlyle, a Scottish writer and historian. Even though he wasn't a mathematician, his ideas inspired this geometric tool. Carlyle circles are especially useful for drawing regular polygons (shapes with all sides and angles equal) using only a ruler and compass.

What is a Carlyle Circle?

A Carlyle circle for the equation x² − sx + p = 0.

Let's say you have a quadratic equation like this:

x² − sx + p = 0

Here, 's' and 'p' are just numbers. For example, in x² − 5x + 6 = 0, 's' would be 5 and 'p' would be 6.

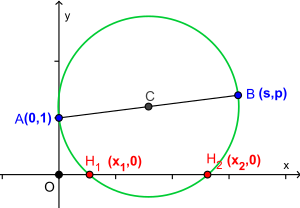
To draw its Carlyle circle, you need two points on a coordinate plane:

• Point A is at (0, 1)
• Point B is at (s, p)

The Carlyle circle is the circle that has the line segment connecting these two points (A and B) as its diameter.

How It Helps Solve Equations

The amazing thing about the Carlyle circle is how it connects to the solutions of a quadratic equation.

When you draw this circle, the points where it crosses the horizontal X-axis are the solutions to the equation x² − sx + p = 0. This means you can find the answers to a math problem just by drawing a circle!

Drawing Regular Polygons

Carlyle circles are very helpful for drawing regular polygons accurately using only a compass and a straightedge (ruler without markings). This is an old challenge in geometry.

Drawing a Regular Pentagon

How to draw a regular pentagon using Carlyle circles.

A pentagon is a shape with five equal sides and five equal angles. Drawing a perfect pentagon can be tricky. Here's how Carlyle circles help:

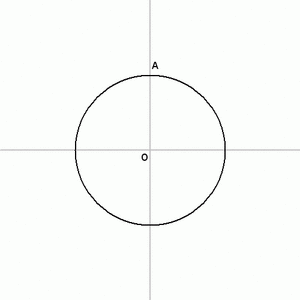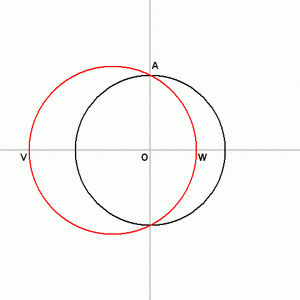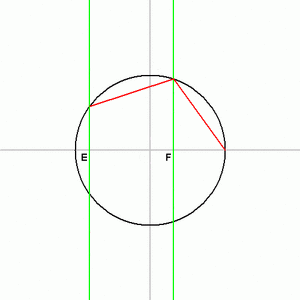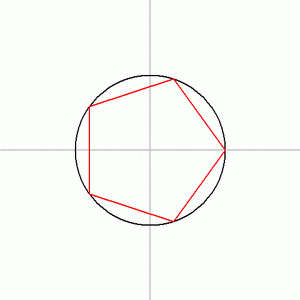
The problem of drawing a regular pentagon is linked to solving a specific quadratic equation:

x² + x − 1 = 0

The Carlyle circle for this equation has its diameter connecting the points (0, 1) and (−1, −1). Its center is at (−1/2, 0). The points where this circle crosses the X-axis help us find the exact lengths needed to draw the pentagon.

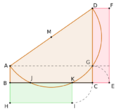
Here are the steps to construct a regular pentagon using a Carlyle circle:

• Draw a large circle. This will be the circle that your pentagon fits inside. Mark its center as point O.
• Draw a horizontal line through the center O. Mark where it crosses the large circle as point B.
• Draw a vertical line through the center O. Mark where it crosses the large circle as point A.
• Find the midpoint of the line segment OB. Call this point M.
• Now, draw a new circle. This is your Carlyle circle. It should be centered at M and pass through point A.
• This Carlyle circle will cross the horizontal line you drew earlier. Mark the intersection point that is inside your original large circle as W. Mark the intersection point that is outside the original large circle as V.
• Using W as your center, draw another circle with a radius equal to OA (the radius of your original large circle). This new circle will cross your original large circle at two points. These are two vertices (corners) of your pentagon.
• Using V as your center, draw another circle with a radius equal to OA. This circle will also cross your original large circle at two more points. These are two more vertices of your pentagon.
• The fifth vertex of the pentagon is where the horizontal line crosses your original large circle (point B).

Connect these five points, and you will have a perfectly regular pentagon!

Other Regular Polygons

Drawing a regular heptadecagon using Carlyle circles.

Drawing a regular 257-gon using Carlyle circles.

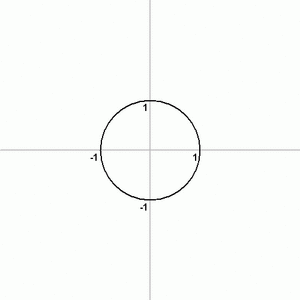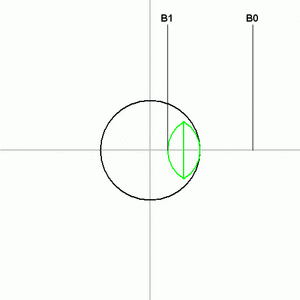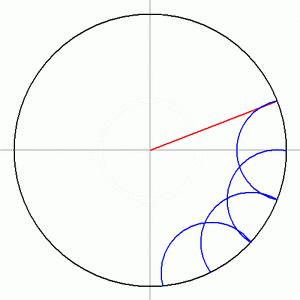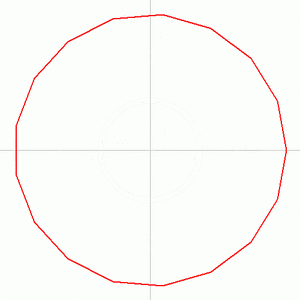
Carlyle circles can also be used to construct other complex regular polygons, such as:

• A regular heptadecagon (a 17-sided polygon).
• A regular 257-gon (a 257-sided polygon). For this, you would need to construct many Carlyle circles (up to 24 of them!).
• A regular 65537-gon (a 65,537-sided polygon). While possible in theory, drawing this many circles and lines would be very difficult in practice!

History of the Carlyle Circle

The idea behind the Carlyle circle has a fascinating history.

• In the early 1800s, a mathematician named John Leslie described a way to use a circle to solve a geometry problem. He said the idea came from his former student, Thomas Carlyle. However, Leslie's description didn't use coordinate systems or quadratic equations as we do today.
• In 1867, an Austrian engineer named Eduard Lill developed a graphical method to find the roots of polynomial equations. His method, when applied to quadratic equations, showed a shape similar to what we now call the Carlyle circle.
• Later, in 1925, G. A. Miller explained the modern definition of the Carlyle circle. He showed how it could be used to find the solutions of quadratic equations geometrically.
• The name "Carlyle circle" became popular after Howard Eves used it in his 1953 book on the history of mathematics.
• In the late 1980s and early 1990s, mathematician DeTemple used Carlyle circles to create step-by-step instructions for drawing regular polygons like the pentagon, heptadecagon, 257-gon, and 65537-gon using only a compass and straightedge.

Carlyle circles show how different areas of mathematics, like algebra (equations) and geometry (shapes), are connected.

Images for kids

• 

  Carlyle's solution to Leslie's problem.