Digon facts for kids
In geometry, a digon is a special type of polygon. It has two sides (also called edges) and two corners (called vertices). Imagine a shape with only two straight lines and two points where they meet – that's a digon!
Usually, polygons like triangles or squares are flat shapes on a flat surface. But a digon is a bit different. On a flat surface, its two sides would either overlap perfectly, or they would have to be curved. This is why it's sometimes called "degenerate" in flat geometry. However, it's easy to see and understand a digon when you think about shapes on a sphere, like the surface of a ball.
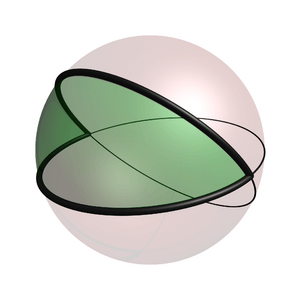
A regular digon is one where both its sides are the same length and both its angles are equal. Mathematicians use a special symbol, {2}, to represent it. You can make a regular digon on a sphere by drawing two lines (which are actually curved arcs) that go halfway around the sphere. These lines connect two points that are exactly opposite each other on the sphere, like the North Pole and the South Pole. When you do this, the digon forms a shape called a spherical lune, which looks like a slice of an orange peel.
The digon is considered the simplest type of "abstract polytope" in a certain way. This means it's a basic building block in the study of shapes with many sides and dimensions.
Contents
What is a Digon?
A digon is a polygon with the fewest possible sides. While we usually think of polygons as having at least three sides (like a triangle), the digon stretches that idea to just two. It helps us understand how shapes can exist in different kinds of spaces, not just flat ones.
Digons on a Sphere
Digons are easiest to understand when you picture them on the surface of a sphere.
- Imagine drawing a line from the North Pole to the South Pole on a globe.
- Now draw another line from the North Pole to the South Pole, but on a different path.
- These two lines form the "sides" of the digon.
- The North Pole and South Pole are the "vertices" (corners) of the digon.
The space between these two lines on the sphere is the digon itself. This curved shape is called a spherical lune.
How Digons Relate to Other Shapes
Even though a digon seems simple, it's connected to more complex shapes in geometry.
- If you "truncate" (cut off the corners of) a digon in a specific way, it can become a square. This is shown by the symbol t{2} which turns into {4} (the symbol for a square).
- If you "alternate" (remove every other vertex of) a digon, it can become a monogon, which is a shape with only one side, represented by {1}. These ideas show how different geometric shapes are related to each other through mathematical operations.
Images for kids
-
A nonuniform rhombicuboctahedron with blue rectangular faces that can become digons.
See also
In Spanish: Dígono para niños
