Dirac delta function facts for kids

What the Dirac delta function looks like

How the Dirac delta function is formed from other shapes

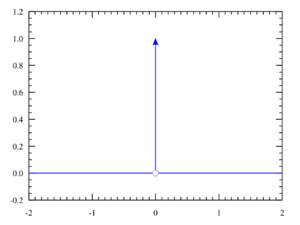
The Dirac delta function, often written as 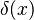, is a special idea in mathematics. It was created by a scientist named Paul Dirac. Think of it like a super-thin, super-tall spike that appears at just one point. Everywhere else, it's completely flat and zero.

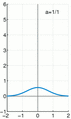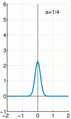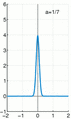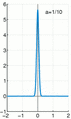
This amazing spike is so special that even though it's zero almost everywhere, the total "area" under it adds up to exactly 1. It's like having a tiny, invisible dot that still holds a lot of power!

This function is very useful in many areas, like when scientists need to take very clear "samples" of information. It helps them focus on one exact moment or point without any extra noise.

What is the Dirac Delta Function?

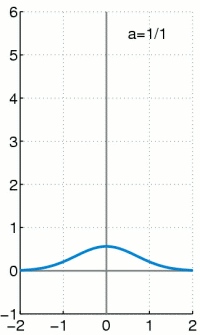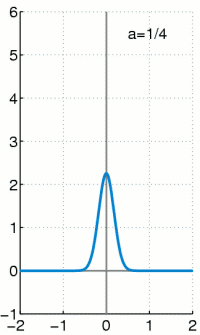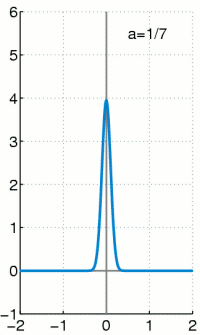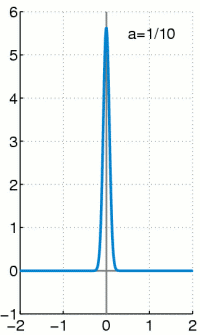
The Dirac delta function is not a "normal" function you might learn about in early math. It's a bit more advanced. Imagine you have a very thin, tall rectangle. Now, imagine making that rectangle even thinner and taller, almost like a needle. The Dirac delta function is what happens when this rectangle becomes infinitely thin and infinitely tall, but its total area always stays at 1.

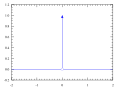
It's zero everywhere except at the poin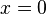t . At 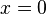, its value is considered to be "infinity." This might sound strange, but it's a powerful tool for describing things that happen instantly or at a single point.

How is it Used?

The Dirac delta function is used in many different fields of science and engineering.

• Signal Processing: Imagine you want to record a very short sound, like a click. The Dirac delta function can help describe this exact moment. It's used in things like digital signal processing to understand quick bursts of information.
• Physics: In physics, it can describe the density of a point mass or a point charge. For example, if you have a tiny, heavy particle, its mass is concentrated at one single point.
• Probability: It can also be used in probability theory to describe events that happen with certainty at a specific value.

Connection to Other Functions

The Dirac delta function is closely related to another important function called the Heaviside function. The Heaviside function is like a switch: it's zero for all negative numbers and then suddenly jumps to one for all positive numbers.

Think of it this way: if you "measure" how quickly the Heaviside function switches from zero to one, you get the Dirac delta function. So, the Dirac delta function can be seen as the "rate of change" or the derivative of the Heaviside function.

Related pages

• Special functions

See also

In Spanish: Delta de Dirac para niños

Images for kids

• 

  Schematic representation of the Dirac delta function by a line surmounted by an arrow. The height of the arrow is usually used to specify the value of any multiplicative constant, which will give the area under the function. The other convention is to write the area next to the arrowhead.

• 

  The Dirac delta function as the limit (in the sense of distributions) of the sequence of zero-centered normal distribution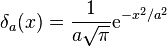s as 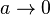.