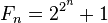Fermat number facts for kids
A Fermat number is a special kind of positive number in mathematics. These numbers are named after a famous French mathematician, Pierre de Fermat. They follow a unique pattern.
You can find a Fermat number using this formula:
Here, n is a whole number that is zero or greater (0, 1, 2, 3, and so on).
Let's look at the first few Fermat numbers:
- F0 = 21 + 1 = 3
- F1 = 22 + 1 = 5
- F2 = 24 + 1 = 17
- F3 = 28 + 1 = 257
- F4 = 216 + 1 = 65537
- F5 = 232 + 1 = 4,294,967,297 (This one is very large!)
As of 2007, only the first 12 Fermat numbers have been completely factored. This means they have been broken down into their prime parts.
Contents
What are Fermat Primes?
A prime number is a whole number greater than 1 that has no positive divisors other than 1 and itself. Examples are 2, 3, 5, 7, 11.
If a number made by the formula 2n + 1 is a prime number, and n is greater than 0, then n must be a power of two. Numbers that are both Fermat numbers and prime numbers are called Fermat primes. The only known Fermat primes are F0, F1, F2, F3, and F4.
Cool Facts About Fermat Numbers
- No Common Divisors: No two different Fermat numbers share any common divisor (a number that divides into them evenly). This is a unique property!
- Recursive Calculation: You can calculate a Fermat number by using the ones before it. To find the Nth Fermat number, you multiply all the Fermat numbers before it and then add two to the result.
How Are Fermat Numbers Used?
Today, Fermat numbers can be helpful in computer science. They are sometimes used to create random numbers. These random numbers are usually between 0 and a specific value that is a power of 2.
Fermat's Idea and Euler's Discovery
When Pierre de Fermat first studied these numbers, he had a guess, or conjecture. He thought that all Fermat numbers would be prime numbers. However, this idea was later proven wrong. In 1732, a mathematician named Leonhard Euler showed that F5 was not a prime number. He found that F5 (which is 4,294,967,297) could be divided by 641 and 6,700,417. Since it has other divisors besides 1 and itself, it is not a prime number.
See also
 In Spanish: Número de Fermat para niños
In Spanish: Número de Fermat para niños
 | Kyle Baker |
 | Joseph Yoakum |
 | Laura Wheeler Waring |
 | Henry Ossawa Tanner |