Fourier transform facts for kids
The Fourier transform is a special math tool. It helps us figure out what basic sounds or waves are mixed together in a complex signal. Imagine you play a chord on a piano. Many notes blend together to make one sound wave. The Fourier transform can take this mixed sound wave and find all the individual notes (or frequencies) that are in it.
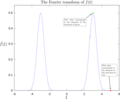
The result of a Fourier transform is often called a frequency spectrum. It shows how much of each frequency is present in the original signal. This tool is used in many areas, like sound design, radiology (for medical images), and even in machine learning and quantum physics.
Contents
How the Fourier Transform Works
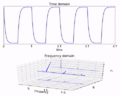
A Fourier transform helps us see what different frequencies are in a signal. For example, think about a sound wave that has three different musical notes: A, B, and C. If you make a graph of the Fourier transform of this sound wave, you would see a peak for each note. The x-axis would show the frequency, and the y-axis would show how strong that frequency is.
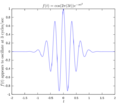
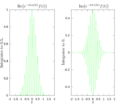
Many signals, like sounds or light waves, can be made by adding together simpler waves called cosines and sines. These simpler waves have different strengths (called amplitudes) and frequencies. The Fourier transform shows you the strengths and phases of these simple waves for each frequency.
Why the Fourier Transform is Important
Fourier transforms are very useful because many signals make more sense when you separate them into their different frequencies. In our sound example, just looking at the sound wave over time doesn't clearly show that notes A, B, and C are playing. But the Fourier transform makes it obvious!
Also, many systems treat different frequencies in different ways. For instance, a "filter" might block high frequencies, letting only low sounds pass through. By using the Fourier transform, we can understand exactly how these systems work on each frequency.
Calculating Fourier Transforms
Calculating a Fourier transform can be complicated. It involves advanced math like integration and imaginary numbers. Because of this, computers are usually used to do these calculations for most real-world signals. A very fast way computers do this is called the Fast Fourier Transform (FFT).
Images for kids
-
This animation shows how a complex wave (red) can be broken down into simpler waves (blue). These simpler waves then appear as peaks in the frequency graph.
-
This image helps explain how complex numbers are used in the Fourier transform. It shows a helix shape, which combines a cosine wave and a sine wave.
-
This animation shows what happens to the Fourier transform when a signal is shifted in time. Notice how higher frequencies spin faster in the complex plane.
-
An original wave signal that moves up and down 3 times per second (3 hertz).
-
The real and imaginary parts of the math for the Fourier transform at 3 hertz.
-
The real and imaginary parts of the math for the Fourier transform at 5 hertz.
-
The Fourier transform of the wave, showing peaks at 3 and 5 hertz.
.gif)
Related topics
See also
In Spanish: Transformada de Fourier para niños
