Giulio Carlo de' Toschi di Fagnano facts for kids
Giulio Carlo Fagnano (born September 26, 1682 – died May 18, 1766) was an important Italian mathematician. He was likely the first person to focus on a special area of math called elliptic integrals. Fagnano was born in a town called Senigallia, and he also passed away there.
Life of Giulio Fagnano
Giulio Fagnano was born in Senigallia, Italy, in 1682. His parents were Francesco Fagnano and Camilla Bartolini.
Giulio Fagnano had twelve children. One of his sons, Giovanni Fagnano, also became a famous mathematician. Another of his children became a nun.
Fagnano received many honors during his life. In 1721, the King of France, Louis XV, made him a count. In 1723, he was chosen to be the gonfaloniere (a high official) of Senigallia. That same year, he was also invited to join the Royal Society of London, which is a very old and respected group of scientists. Later, in 1745, he was given the title of marquis.
Giulio Fagnano's Math Work
Giulio Fagnano studied at the Collegio Clementino in Rome. He did very well in his studies, except for mathematics. At first, he really didn't like math!
However, after finishing college, he decided to try learning mathematics. He taught himself everything from the very basics, without any teachers. Most of his important math discoveries were published in a journal called Giornale de' Letterati d'Italia.
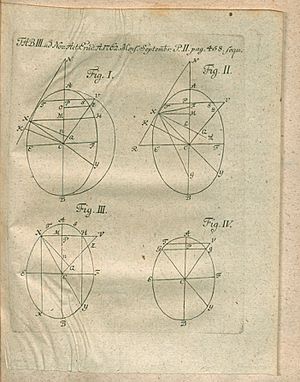
Fagnano is best known for his work on measuring and dividing parts of curves. He was especially interested in a curve called the lemniscate. He thought this was his most important work.
He even had a picture of the lemniscate curve engraved on the title page of his book, Produzioni Matematiche. This book was published in two volumes in 1750 and was dedicated to Pope Benedict XIV. The same picture and words also appear on his tomb.
Fagnano tried to find the exact length of parts of curves like the ellipse and hyperbola. When he couldn't find the exact length, he tried to find arcs (parts of curves) whose difference in length could be found.
He also noticed how similar the math used to find the length of a circle's arc was to the math used for a lemniscate's arc. This was a very important discovery for future mathematicians.