Identity (mathematics) facts for kids
In mathematics, the word identity has a few important meanings. It can mean an equation that is always true, no matter what numbers you put in. It can also mean a special number or item that doesn't change other numbers or items when you combine them.
Here are the main ways "identity" is used in math:
- An identity can be an equation that stays true even if you change the values of the variables in it. Think of it like a rule that always works.
- In algebra, an identity element is a special item that doesn't change another item when they are combined using a certain math operation.
- The identity function is a type of function that simply gives you back the same number you put in.
- In linear algebra, the identity matrix is a special kind of grid of numbers that doesn't change other matrices when you multiply them.
Contents
What is an Identity Equation?
An identity equation is a math statement that is always true. It's different from a regular equation that might only be true for certain numbers.
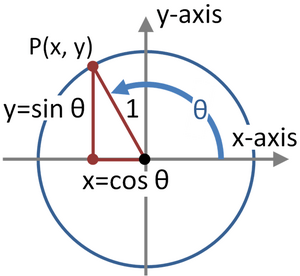
For example, the trigonometric identity below is always true for any real number you use for theta (θ): 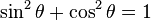Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sin ^2 \theta + \cos ^2 \theta = 1\,
This means if you pick any angle θ, find its sine and cosine, square them, and add them up, you will always get 1.
But if you look at an equation like: 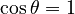Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \cos \theta = 1\,
This is only true for specific angles, like 0 degrees, 360 degrees, or 720 degrees. It's not true for all angles. So, it's an equation, but not an identity.
What is an Identity Element?
An identity element is a special number or item that, when combined with another item using a specific operation, leaves the other item unchanged.
Additive Identity
The number 0 is the "additive identity." This means that when you add 0 to any number, the number stays the same.
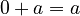
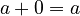
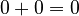
For example, with real numbers: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 0 + a = a\, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a + 0 = a\, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 0 + 0 = 0\,
No matter what number 'a' is, adding 0 to it (or adding 'a' to 0) doesn't change 'a'.
Multiplicative Identity
The number 1 is the "multiplicative identity." This means that when you multiply any number by 1, the number stays the same.
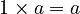
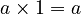
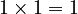
For example, with real numbers: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1 \times a = a\, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a \times 1 = a\, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1 \times 1 = 1\,
No matter what number 'a' is, multiplying it by 1 (or multiplying 1 by 'a') doesn't change 'a'.
What is an Identity Function?
An identity function is a simple type of function. It takes an input and gives you the exact same input back as the output.
You can think of it like a mirror. Whatever you show it, it shows you back. If you put 'x' into the identity function, you get 'x' out.
A common example is the identity permutation. This is a way of arranging things where each item stays in its original spot. For example, if you have numbers {1, 2, 3}, the identity permutation just keeps them as {1, 2, 3}.
How are These Meanings Connected?
Sometimes, these different meanings of "identity" can be related. For example, the identity permutation (which is an identity function) can also be seen as the identity element in the group of all possible arrangements (permutations) when you combine them in a certain way.
See also
In Spanish: Identidad (matemática) para niños
