Linear mapping facts for kids
A linear mapping is a special kind of function in mathematics. It's also called a linear transformation. Imagine you have a shape, and you want to stretch it, rotate it, or flip it. A linear mapping describes these kinds of changes. It moves points from one vector space to another. The cool thing is, it does this while keeping straight lines straight and the origin (the point 0,0) in place.
What is a Linear Mapping?
A linear mapping is a rule that connects two vector spaces. Let's call these spaces V and W. Think of vector spaces as collections of "arrows" or "directions" (called vectors) that you can add together or stretch.
A function f that goes from space V to space W is a linear mapping if it follows two important rules:
- Rule 1: Addition is preserved
When you add two vectors (let's call them x and y) in space V and then apply the mapping f, the result is the same as if you applied f to each vector first and then added their results.
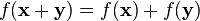 |
This means if you combine two movements and then transform them, it's the same as transforming each movement separately and then combining the results.
- Rule 2: Scalar multiplication is preserved
A "scalar" is just a regular number, like 2 or 5. If you take a vector x and stretch it by a scalar (say, α), and then apply the mapping f, it's the same as applying f to the vector first and then stretching the result by the same scalar.
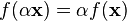 |
This means if you scale something and then transform it, it's the same as transforming it and then scaling the result.
Sometimes, people call a linear mapping a "linear function." But be careful! In basic math, a linear function usually means a function whose graph is a straight line, like y = 2x + 3. A linear mapping is a more general idea used in higher math.
Why are Linear Mappings Important?
Linear mappings are super useful in many areas, like:
- Computer Graphics: They help computers rotate, scale, and move 3D objects on a screen.
- Physics: They describe how forces act on objects or how systems change over time.
- Engineering: They are used in signal processing, control systems, and robotics.
- Data Science: They help analyze and transform large sets of data.
They are fundamental because they describe simple, predictable transformations that don't distort space in complicated ways.
Related Concepts
- Homomorphism: This is a more general idea in math. A linear mapping is a specific type of homomorphism for vector spaces.
- Transformation: This is a general term for any function that changes one object into another. A linear mapping is a specific kind of transformation.
See also
 In Spanish: Aplicación lineal para niños
In Spanish: Aplicación lineal para niños

