kids encyclopedia robot

Magma (mathematics) facts for kids

Kids Encyclopedia Facts

A magma is a basic idea in mathematics. Think of it as a special way to organize a set (which is just a collection of things, like numbers) along with a rule for combining those things.

This rule is called a binary operation. A binary operation takes any two items from your set and combines them to make one new item that is also in the same set. It's like a math machine: you put two numbers in, and it gives you one number out.

If we call our set X and our combining rule • (like a dot), then we write the magma as (X, •).

What are Magmas? Examples in Math

Let's look at some examples to understand magmas better.

Natural Numbers and Addition

The natural numbers are numbers like 1, 2, 3, 4, and so on. If we take any two natural numbers and add them, the answer is always another natural number.

  • For example, 3 + 5 = 8. Both 3, 5, and 8 are natural numbers.
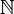  • The set of natural numbers is written as \mathbb{N}.
  • Addition is written as +.
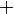  • So, the natural numbers with addition form a magma, written as 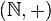(\mathbb{N} , +). We can call this "The natural numbers under addition."

Integers and Multiplication

The integers include all whole numbers, positive, negative, and zero (..., -2, -1, 0, 1, 2, ...). If we multiply any two integers, the result is always another integer.

  • For example, -4 × 3 = -12. All these numbers are integers.
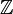  • The set of integers is written as \mathbb{Z}.
  • Multiplication in abstract math is often written as \cdot.
  • So, the integers with multiplication form a magma, written as 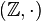(\mathbb{Z}, \cdot). This is called "The integers under multiplication."

Real Numbers and Division

The real numbers include all numbers you can think of, like 1, -5, 3.14, and even numbers like the square root of 2.

  • Do real numbers with division form a magma? Not quite!
  • The rule for a binary operation says you must be able to combine any two elements.
  • The problem with division is that you cannot divide by zero. For example, 5 ÷ 0 doesn't give you a real number.
  • Because of this one exception (dividing by zero), the real numbers under division do not form a magma.

Real Numbers (without Zero) and Division

However, we can make a magma if we change the set slightly.

  • If we take all real numbers except zero, then division works perfectly!
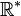  • This set is written as \mathbb{R}^*.
  • In this case, 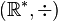(\mathbb{R}^*, \div) is a magma. This shows how important it is to define the set and the operation carefully.
kids search engine
All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:
Magma (mathematics) Facts for Kids. Kiddle Encyclopedia.