Power series facts for kids

A power series is a special kind of infinite series in mathematics. Think of it like a very long polynomial that never ends! It has terms that include powers of a variable, like x, x², x³, and so on, multiplied by different numbers.

These series are often "centered" around a specific number. This means the variable in the series is written as (x - c), where c is that specific number. If c is zero, the series becomes simpler, just using x, x², x³, etc.

Power series are super useful! They help mathematicians and scientists understand and work with many different functions. For example, they are used to represent complex functions in a simpler way, making them easier to study.

What is a Power Series?

Imagine you have a list of numbers that goes on forever. A power series is like that, but each number in the list is part of a pattern. It starts with a regular number, then adds another number multiplied by x, then another number multiplied by x², and so on.

Here's how it generally looks, without the complex math symbols:

• A number (let's call it a₀)
• Plus another number (a₁) times x
• Plus another number (a₂) times x²
• Plus another number (a₃) times x³
• And this pattern continues forever!

So, it's like: a₀ + a₁x + a₂x² + a₃x³ + ...

The numbers a₀, a₁, a₂, etc., are called coefficients. They are just regular numbers that tell you how much of each x term to add.

Where Are Power Series Used?

Power series show up in many areas of math and science.

Representing Functions

One of their main uses is to represent functions. Many important functions, like the exponential function or sine and cosine, can be written as power series. This is especially helpful because it allows us to approximate these functions using just a few terms of the series, which is much easier to calculate.

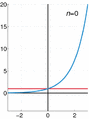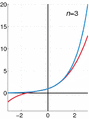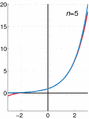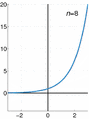
For example, a famous type of power series is called a Taylor series. It helps us turn complicated functions into these simpler, never-ending polynomial-like forms.

Other Uses

• Combinatorics: This is a branch of math about counting. Power series are used here as "generating functions" to solve counting problems.
• Electrical Engineering: In this field, power series are used in something called the Z-transform, which helps analyze signals and systems.
• Number Systems: Even our everyday decimal notation for numbers can be seen as a type of power series. For example, the number 345 is really (3 × 10²) + (4 × 10¹) + (5 × 10⁰). This is a power series where x is 10.
• Number Theory: In advanced number theory, power series are related to p-adic numbers, which are a different way of looking at numbers.

Images for kids

• 

  The exponential function (in blue), and the sum of the first n + 1 terms of its Maclaurin power series (in red).

See also

In Spanish: Serie de potencias para niños