Angular momentum facts for kids
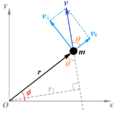
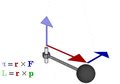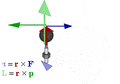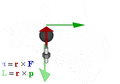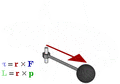
Angular momentum is a way to measure how much an object is spinning or orbiting. Think of it as an object's "spinning power." It depends on two main things:
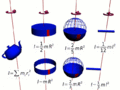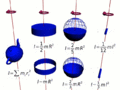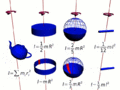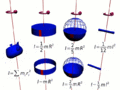
- How spread out the object's mass is from its spinning center (this is called its moment of inertia).
- How fast the object is spinning or orbiting (this is its angular velocity).
There are two main types of angular momentum: spin angular momentum and orbital angular momentum.
Spin Angular Momentum
Spin angular momentum is about objects that spin around an axis that goes right through them. Imagine a toy top spinning in place or a basketball spinning on your finger. The axis of rotation is inside the object itself.
Objects that have their mass spread far out from their center are harder to start spinning. But once they are spinning, they are also harder to stop. This is because they have a large moment of inertia. It's also easier to make something spin slowly than to make it spin very fast. So, spin angular momentum depends on both how spread out the object is and how quickly it's spinning.
Orbital Angular Momentum
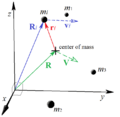
Orbital angular momentum is different. This type of angular momentum describes objects that orbit around a point or another object. A great example is how planets orbit around the Sun. The Sun is the center point, and the planets move around it.
When we talk about orbital angular momentum, we mean an object moving in a circle or ellipse around something else. Part of its movement is always going around that central point. Orbital angular momentum also tells us how hard it would be to stop the object from continuing its orbit.
Angular momentum is a conserved quantity. This means that an object's angular momentum will stay the same unless an outside force, called a torque, acts on it. A torque is like a twisting force that can change how something spins or orbits.
Related pages
Images for kids
See also
 In Spanish: Momento angular para niños
In Spanish: Momento angular para niños