Schwarzschild metric facts for kids
The Schwarzschild metric is a special equation from general relativity, a theory by Albert Einstein. It was figured out by a scientist named Karl Schwarzschild in 1916.
Think of it like a map for spacetime around a black hole. This specific equation describes the gravitational field around a special kind of black hole called a Schwarzschild black hole. This type of black hole doesn't spin, is perfectly round, and doesn't have a magnetic field.
Basically, the Schwarzschild metric helps us understand how things move and how time behaves in the super strong gravity near a black hole.
Contents
What is a Metric?
In physics, a metric is like a rulebook that tells us how to measure distances and time in spacetime. Spacetime is the four-dimensional world we live in, combining space (length, width, height) and time.
The Schwarzschild metric is a very important tool for studying black holes because it helps scientists predict how light and objects will behave when they get close to these incredibly dense objects.
Understanding the Equation
The full equation looks complicated: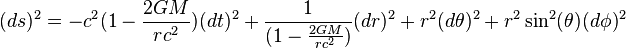 
But let's break down what some of the letters mean:
- c is the speed of light. It's the fastest speed anything can travel in the universe.
- G is the gravitational constant. It's a number that tells us how strong gravity is.
- M is the mass of the black hole. The more mass a black hole has, the stronger its gravity.
- r is the distance from the center of the black hole.
- ds, dt, dr, dθ, dφ are tiny changes in path, time, distance, and angles.
This equation helps scientists calculate the path of a particle as it moves through the curved spacetime around a black hole.
The Schwarzschild Radius
One very important idea that comes from the Schwarzschild metric is the Schwarzschild radius (often written as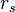 
).
The Schwarzschild radius is like a special boundary around a black hole. If anything, even light, crosses this boundary, it can't escape the black hole's gravity. This boundary is also known as the event horizon.
The Schwarzschild radius depends on the mass of the object. For example, if our Sun were to become a black hole, its Schwarzschild radius would be about 3 kilometers (less than 2 miles)!
While it's most famous for black holes, you can actually calculate a Schwarzschild radius for any object with mass. For Earth, it would be less than a centimeter, meaning Earth would have to be squished incredibly small to become a black hole.
Images for kids
-
This picture shows a model called Flamm's paraboloid. It helps us imagine how spacetime is curved around a heavy object like a black hole.
See also
In Spanish: Métrica de Schwarzschild para niños
