Second derivative Facts for Kids

The second derivative is a cool idea in mathematics and physics! Imagine you have a function, which is like a rule that tells you how one thing changes as another thing changes. The first derivative tells you how fast something is changing. For example, if you're driving a car, your speed is the first derivative of your position.

Now, the second derivative tells you how fast that rate of change is changing. So, if your speed is changing (you're speeding up or slowing down), that's what the second derivative helps us understand. In the car example, the second derivative of your position is your acceleration! It shows if you're pushing the gas pedal harder or hitting the brakes.

You might see the second derivative written in a few ways, like:

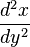\frac{d^2x}{dy^2}

f''(x)

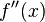
These are just different ways mathematicians write the same idea.

Understanding the Power Rule for Second Derivatives
What the Second Derivative Tells Us
- Concavity: Is the Graph Smiling or Frowning?
- Inflection Points: Where the Smile Changes to a Frown
Real-World Uses of the Second Derivative
See also

Understanding the Power Rule for Second Derivatives

When you have a simple function like 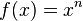$f(x)=x^n$ (where 'n' is just a number), you can find its second derivative using something called the power rule.

Think of it like this:

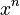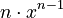The first derivative of $x^n$ is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): n \cdot x^{n-1} . You bring the power down and subtract one from the power.
To get the second derivative, you do that again! You take the derivative of the first derivative.

So, for 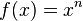$f(x)=x^n$ , the second derivative is 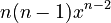Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): n(n-1)x^{n-2} . This rule helps us quickly find how the rate of change is changing for many simple functions.

What the Second Derivative Tells Us

The second derivative is super useful because it helps us understand the shape of a function's graph.

Concavity: Is the Graph Smiling or Frowning?

The second derivative tells us about something called concavity.

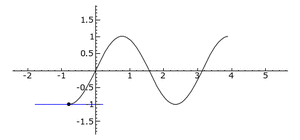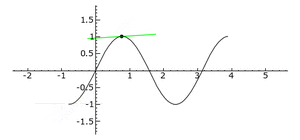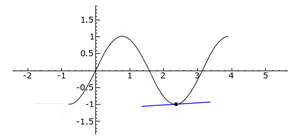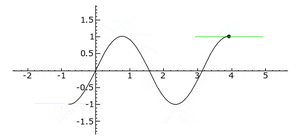
If the second derivative is positive (greater than zero), the graph of the function looks like a "cup" or a "smile" (it's concave up). Imagine a bowl holding water.
If the second derivative is negative (less than zero), the graph looks like an "upside-down cup" or a "frown" (it's concave down). Imagine a hill.

Inflection Points: Where the Smile Changes to a Frown

An inflection point is a special spot on a graph where the concavity changes. This means the graph switches from being concave up to concave down, or vice versa. At these points, the second derivative is often zero or undefined.

Think of it like a roller coaster:

When you're going up a curve that's bending upwards, that's concave up.
When you're going down a curve that's bending downwards, that's concave down.
An inflection point is where the track changes how it's bending, like going from curving up to curving down.

This animation shows how the curve changes its bend. The red points are inflection points where the concavity changes.

Real-World Uses of the Second Derivative

The second derivative isn't just for math class; it has many uses in the real world!

Acceleration and Motion

As we talked about, the second derivative is key to understanding acceleration.

If you know a car's position over time, the first derivative gives you its speed.
The second derivative gives you its acceleration – how quickly its speed is changing. This is important for designing vehicles, understanding how objects fall, and even planning space missions!

Optimization: Finding Best Outcomes

In many fields, people use the second derivative to find the "best" or "worst" points.

For example, a company might use it to find the maximum profit or the minimum cost.
Engineers might use it to find the strongest design for a bridge or the most efficient way to use materials.
If the second derivative is positive at a critical point, it means you've found a local minimum (the bottom of a dip).
If it's negative, you've found a local maximum (the top of a peak).

Science and Engineering

In physics, it helps describe forces and energy.
In engineering, it's used in designing structures, understanding vibrations, and controlling systems.
In economics, it can help predict how markets will change.

The second derivative is a powerful tool that helps us understand how things change and how those changes themselves are changing!

Second derivative facts for kids

Contents