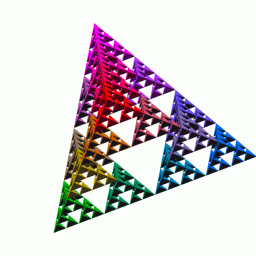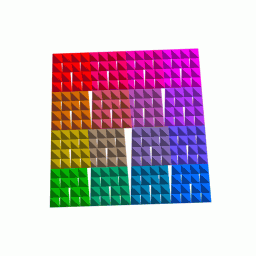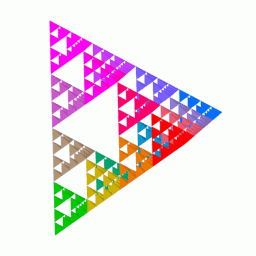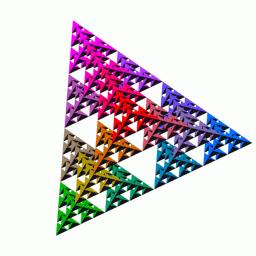Sierpiński triangle facts for kids
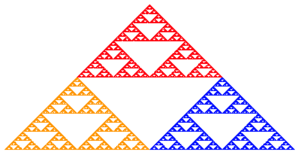
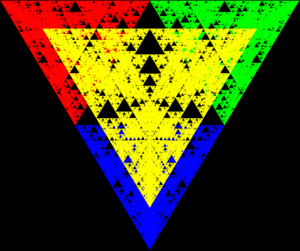
The Sierpiński triangle is a special kind of shape called a fractal. Imagine a triangle that keeps repeating itself, getting smaller and smaller. That's what a fractal is! The Sierpiński triangle looks like a big triangle made up of many smaller triangles. It's famous for being "self-similar," meaning it looks the same no matter how much you zoom in or out.
This cool shape is named after a Polish mathematician named Wacław Sierpiński. He wrote about it in 1915. But people had used similar patterns in art and decorations many centuries before him!
Contents
How to Make a Sierpiński Triangle
There are several fun ways to create the Sierpiński triangle.
Removing Triangles
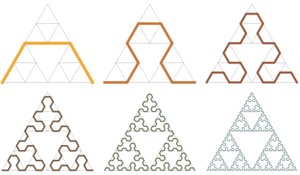
You can make a Sierpiński triangle by taking away parts of a regular triangle:
- Start with a large, flat triangle where all sides are equal (an equilateral triangle).
- Imagine dividing this big triangle into four smaller, equal triangles.
- Now, take out the middle triangle. You'll be left with three smaller triangles at the corners.
- Repeat this step! For each of the three remaining triangles, divide it into four smaller ones and remove its middle part.
- If you keep doing this forever, you'll end up with the Sierpiński triangle!
Shrinking and Copying
You can also make the Sierpiński triangle by shrinking and copying triangles:
- Start with any triangle. A good way is to use an equilateral triangle.
- Shrink the triangle to half its height and half its width.
- Make three copies of this smaller triangle.
- Arrange these three small triangles so that each one touches the other two at a corner. You'll notice a hole appears in the middle! This is because the three small triangles only cover three-quarters of the original triangle's area.
- Now, repeat this process for each of the three smaller triangles. Shrink them, copy them, and arrange them.
If you keep doing this forever, the shape you get will be the Sierpiński triangle. It's amazing because you can start with almost any shape, and it will still turn into a Sierpiński triangle after many steps!
The Chaos Game
The "chaos game" is a cool way to draw the Sierpiński triangle using random choices:
- First, draw three points on a piece of paper to make a triangle. These are your "corner points."
- Pick any point inside the triangle. This is your "current spot."
- Now, randomly choose one of your three corner points.
- Move your "current spot" exactly halfway between your current spot and the corner point you just chose.
- Draw a dot at this new "current spot."
- Repeat from step 3 over and over again!
Even though you're choosing points randomly, a beautiful Sierpiński triangle will start to appear! After drawing just a hundred dots, you'll see the outline. After a few hundred, the details will really show up. This method is a great example of how simple rules can create complex and beautiful patterns.
Arrowhead Curve
You can also think of the Sierpiński triangle as a special kind of line or "curve."
- Start with a single straight line.
- Now, replace that line with three shorter lines. These new lines form 120-degree angles where they meet, like a zigzag.
- Keep repeating this! For every straight line segment you have, replace it with the same three-segment zigzag pattern.
As you do this more and more, the line becomes super wiggly. In the end, it traces out the entire Sierpiński triangle in one continuous path! This special path is called the Sierpiński arrowhead.
Pascal's Triangle
Have you ever seen Pascal's triangle? It's a triangle made of numbers. If you take Pascal's triangle and color the numbers:
- Color all the even numbers white.
- Color all the odd numbers black.
If you do this for a very large Pascal's triangle, the black and white pattern will look just like the Sierpiński triangle!
What are its Features?
The Sierpiński triangle has some interesting features:
- Dimension: It's not quite 1D (like a line) or 2D (like a flat shape). Its special "fractal dimension" is about 1.585. This means it's more complex than a line but less complex than a solid triangle.
- Area: Even though it looks like it has area, if you keep removing triangles forever, the actual area of the Sierpiński triangle becomes zero! This is because you're always taking away more and more space.
Sierpiński Shapes in 3D
Just like the Sierpiński triangle is a 2D fractal, there's a 3D version called the Sierpiński tetrahedron (or tetrix).
- You start with a shape called a tetrahedron (a pyramid with four triangular faces).
- You shrink it to half its size.
- Then, you put together four copies of this smaller tetrahedron so their corners touch.
- You keep repeating this process.
The Sierpiński tetrahedron is amazing because its total outer surface area stays the same, even as you keep making it more complex! But its total volume (the space it takes up) gets smaller and smaller, eventually becoming zero.
History of the Sierpiński Triangle
Wacław Sierpiński first wrote about this triangle in 1915. However, patterns that look very similar to the Sierpiński triangle were used in art and decorations many centuries before that. For example, you can find similar designs in 13th-century stonework in Italy.
What Does "Gasket" Mean?
Sometimes, the Sierpiński triangle is called the "Sierpiński gasket." The word "gasket" refers to parts found in engines that prevent leaks. These gaskets sometimes have many holes of different sizes, which reminded the mathematician Benoit Mandelbrot of the fractal's many empty spaces. He thought the fractal looked like "the part that prevents leaks in motors," so the name stuck!
See Also
 In Spanish: Triángulo de Sierpinski para niños
In Spanish: Triángulo de Sierpinski para niños
- Sierpiński carpet, another cool fractal named after Sierpiński.
- Triforce, a famous symbol from the Legend of Zelda video games that looks like a Sierpiński triangle.