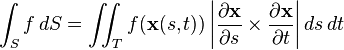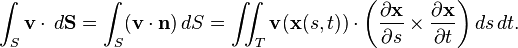Surface integral Facts for Kids

Imagine you want to measure something across a curved surface, like the skin of an apple or the surface of a ball. In mathematics, a surface integral is a special kind of measurement that lets you do just that. It's like a line integral which measures things along a line, but a surface integral measures things over a two-dimensional surface.

You can use surface integrals to measure different things:

Scalar fields: These are like measuring the temperature or density at every point on a surface. The result is a simple number.
Vector fields: These are like measuring the direction and strength of wind or water flow at every point on a surface. The result can be a number (like how much fluid flows through) or a vector (like the total force).

Surface integrals are very important in physics, especially when studying electromagnetism, which deals with electricity and magnetism.

The idea of a surface integral is to break the surface into many tiny pieces.

This picture shows one tiny piece of a surface. We make these pieces super small to get an accurate measurement.

Measuring Scalar Fields on a Surface
Measuring Vector Fields on a Surface
Important Ideas About Surface Integrals
Related Topics
See also

Measuring Scalar Fields on a Surface

Let's say you have a surface, like a thin sheet of metal, and you want to know its total mass. If you know the density (how much material is in a certain area) at every point on the sheet, you can use a surface integral to find the total mass.

Here's how it works:

You imagine splitting the surface into many, many tiny pieces.
For each tiny piece, you pretend the density is the same everywhere on that piece.
You then multiply the density of that piece by its tiny area to find its mass.
Finally, you add up the masses of all these tiny pieces to get the total mass of the whole surface.

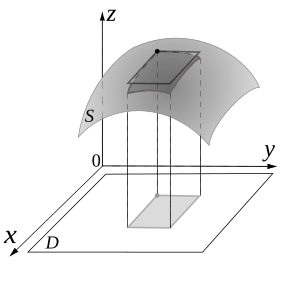
Mathematicians use special formulas to do this. They describe the surface using a "map" or a "parametrization". Think of it like using latitude and longitude to find any point on a sphere.

The formula looks like this:

\int_{S} f \,dS = \iint_{T} f(\mathbf{x}(s, t)) \left|{\partial \mathbf{x} \over \partial s}\times {\partial \mathbf{x} \over \partial t}\right| ds\, dt

This formula helps calculate the total amount of something (like mass or heat) spread across a curved surface. The part with the `x` symbol helps measure the tiny area of each piece of the surface.

For example, if you want to find the total surface area of a curved shape, you can use a similar formula:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{align} A &{} = \iint_T \sqrt{\left({\partial f \over \partial x}\right)^2+\left({\partial f \over \partial y}\right)^2+1}\, \, dx\, dy \end{align}

This formula helps you find the area of a curved surface, like the top of a dome. The terms inside the square root are related to how steep the surface is in different directions.

These formulas work best for surfaces that are in a 3D space.

Measuring Vector Fields on a Surface

This image shows a vector field on a surface. The arrows show the direction and strength of something, like wind or water flow.

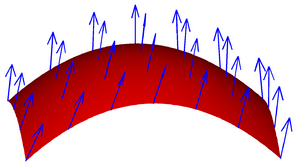
Imagine you have a vector field on a surface. This means at every point on the surface, there's an arrow (a vector) showing a direction and a strength. For example, it could show the velocity (speed and direction) of water flowing through a net.

One common use of surface integrals for vector fields is to calculate the flux. Flux is the amount of something (like fluid or an electric field) passing through a surface in a certain amount of time.

Think about water flowing through a net:

If the water flows parallel to the net (just skimming along it), no water actually passes through the net. The flux is zero.
If the water flows straight through the net, you get the maximum flux.
If the water flows at an angle, only the part of the flow that goes directly through the net counts towards the flux.

To find the flux, mathematicians look at the part of the vector field that is perpendicular (at a right angle) to the surface at each point. This is called the "normal component". They then integrate this normal component over the entire surface.

The formula for flux looks like this:

\int_S {\mathbf v}\cdot \,d{\mathbf {S}} = \int_S ({\mathbf v}\cdot {\mathbf n})\,dS=\iint_T {\mathbf v}(\mathbf{x}(s, t))\cdot \left({\partial \mathbf{x} \over \partial s}\times {\partial \mathbf{x} \over \partial t}\right) ds\, dt.

Here, `v` is the vector field (like the water's velocity), and `n` is the direction that is straight out from the surface. The dot product `v ⋅ n` finds how much of the vector field is pointing directly through the surface.

Important Ideas About Surface Integrals

Surface integrals are powerful tools, and there are some important things to know about how they work:

How We Describe the Surface Matters

When we calculate a surface integral, we often use a "map" or a "parametrization" to describe the surface. For example, we might use latitude and longitude for a sphere. What if we use a different map?

For scalar fields (like density), the answer to the integral will always be the same, no matter which map you use.
For vector fields (like fluid flow), it's a bit trickier. The direction you choose for the "normal" (the line pointing straight out from the surface) matters. If you pick a normal pointing one way, you get a certain answer. If you pick it pointing the exact opposite way, your answer will be the negative of the first one. So, you need to decide on a consistent "outward" or "inward" direction for your surface before you start.

Breaking Surfaces into Pieces

Sometimes, a surface is too complicated to describe with just one map. Imagine a cylinder (like a soda can). You might need one map for the curved side and separate maps for the top and bottom circles.

The solution is to break the surface into smaller pieces, calculate the surface integral for each piece, and then add them all up. When doing this for vector fields, it's important to make sure the "normal" directions for all the pieces are consistent. For a cylinder, if you say the normal points "out" from the side, then the normals for the top and bottom circles should also point "out" from the can.

Surfaces That Are Tricky

Some surfaces are very unusual and don't have a consistent "outside" or "inside" direction. A famous example is the Möbius strip, which only has one side! On such surfaces, it's impossible to consistently define a normal vector at every point. These are called "non-orientable" surfaces. You cannot calculate surface integrals of vector fields on these kinds of surfaces because you can't decide which way the "normal" should point.

Surface integral facts for kids

Contents