Surjective function facts for kids
A surjective function (say that as "sur-JECT-iv") is a special type of function in mathematics. You can also call it an onto function.
Imagine you have two groups of things. A function takes each thing from the first group (called the domain or input set) and matches it to exactly one thing in the second group (called the codomain or output set).
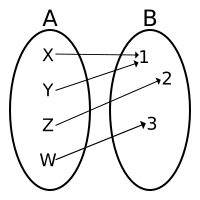 |
| This picture shows a surjection. Every element in the output group (B) has at least one arrow pointing to it from the input group (A). |
For a function to be surjective, every single item in the output group (the codomain) must have at least one arrow pointing to it from the input group. This means no item in the output group is left out or "unmapped." The set of all actual outputs (called the range) is exactly the same as the entire output group (the codomain).
The words surjection, injection, and bijection were first used by a group of mathematicians called Nicolas Bourbaki. They published many books on advanced math in the 1930s. The French word "sur" means "above" or "onto." This makes sense because a surjective function maps its input group onto its entire output group.
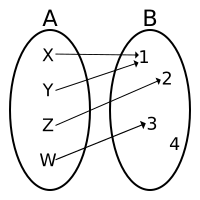 |
| This is not a surjection. The number {4} in the output group (B) has no arrow pointing to it from the input group (A). |
Contents
What a Surjection Means
In simpler terms, a function f from set A to set B is surjective if:
- Every element in the output set B is the result of at least one element from the input set A.
- Every element in the output set B has at least one "pre-image" in the input set A. A pre-image is an input that leads to that specific output.
It's important to know that a pre-image does not have to be unique. Look at the first picture: both {X} and {Y} are pre-images of the number {1}. What matters is that there is at least one pre-image for every output.
Examples of Surjective Functions
Let's look at some examples using numbers. We'll use functions where both the input and output are real numbers (any number, including decimals and negative numbers).
Graphs and Equations
- Looking at a graph: A function is surjective if you can draw any horizontal line across its graph, and that line will always touch the graph in at least one spot.
- Looking at an equation: A function f is surjective if, for any output number y you pick, you can always find at least one input number x that makes f(x) = y.
Finding an input x for a given output y is like solving the equation f(x) = y for x.
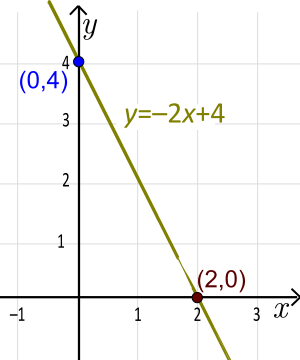
Slanted Lines
Example: A straight line that is slanted (not flat or straight up and down) is always a surjection. For example, the function y = 2x + 1 is surjective.
- Why? No matter what y value you choose, you can always find an x value that works. If y = 5, then 5 = 2x + 1, so 4 = 2x, and x = 2. So, 2 is the input that gives you 5. You can always do this for any y.
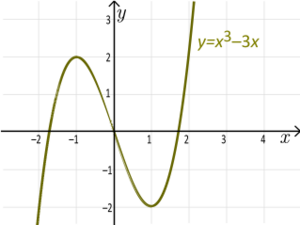
Cubic Functions
Example: The function f(x) = x3 - 3x is a surjection.
- Why? If you graph this function, you'll see it goes up forever and down forever. This means it covers all possible y values. For any y you pick, you can always find at least one x that gives you that y.
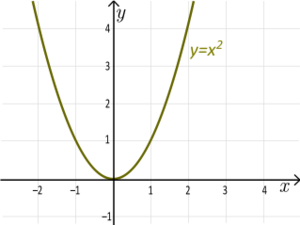
Quadratic Functions (Not Surjective)
Example: The function f(x) = x2 is not a surjection.
- Why? If you try to find an x such that x2 = -1, you can't, because squaring any real number always gives a positive result or zero. So, negative numbers like -1 are not in the output of this function. The range of x2 is only numbers greater than or equal to zero.
Important Note: You can make a non-surjective function into a surjection by changing its output group (codomain). For example, if we say the function f(x) = x2 only outputs numbers greater than or equal to zero, then it becomes surjective!
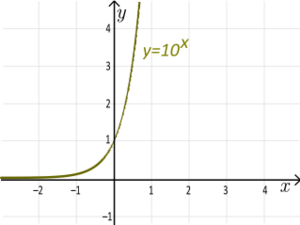
Exponential Functions (Not Surjective)
Example: The exponential function f(x) = 10x is not a surjection.
- Why? The result of 10 raised to any power will always be a positive number. It can never be zero or a negative number. So, if you pick y = -5, there's no x that makes 10x = -5. The range of 10x is only positive numbers.
Other Examples
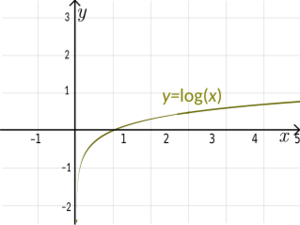
- The logarithmic function f(x) = log(x) (base 10) is a surjection. It's the opposite of 10x, and it can output any real number.
- In 3D video games, the way 3D space is shown on a 2D screen uses a surjection. Many different points in 3D space can end up at the same spot on your screen.
Related pages
See also
 In Spanish: Función sobreyectiva para niños
In Spanish: Función sobreyectiva para niños