Injective function facts for kids
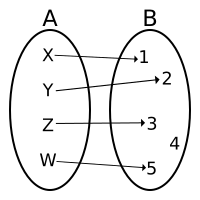 |
| Injection. Think of it like this: each output (in set B) gets at most one arrow pointing to it from an input (in set A). |
In mathematics, an injective function (say, f) is a special kind of function. Imagine you have two groups of things, let's call them Group A (the domain or inputs) and Group B (the codomain or possible outputs).
For a function to be injective, it means that for every item in Group B, there's at most one item in Group A that points to it. In simpler words, if you pick two different items from Group A, they will always point to two different items in Group B. No two different inputs can ever have the same output!
This idea was first introduced by a group of mathematicians called Nicholas Bourbaki in the 1930s.
An injective function is often called a one-to-one (or 1-1) function. But be careful! This is different from a "one-to-one correspondence," which is a special function that is both injective and surjective (meaning every output has an input, and no two inputs share an output).
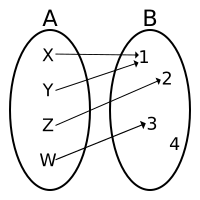 |
| Not an injection. Here, two inputs (X and Y) from set A both point to the same output (1) in set B. |
Contents
What Makes a Function Injective?
A function f from set A to set B is injective if:
- If you have two different inputs from set A, say a1 and a2, then their outputs, f(a1) and f(a2), must also be different.
- Or, looking at it another way: if two inputs give you the same output, then those two inputs must have been the same input to begin with!
When an input a from set A points to an output b in set B (so f(a) = b), we call a a pre-image of b. For injective functions, each output b in set B can have either one pre-image or no pre-images at all. It can never have two or more!
Understanding Cardinality
Cardinality is just a fancy word for the number of elements in a set. For example, if you have a set A = {apple, banana, cherry}, its cardinality is 3. We write this as #A = 3.
If the number of possible outputs (the cardinality of the codomain) is less than the number of inputs (the cardinality of the domain), then the function cannot be injective.
- Imagine you have 6 students (inputs) and only 5 chairs (outputs). If each student needs a chair, at least two students will have to share a chair. This means it's impossible for each student to have their own unique chair.
- In math terms, you can't map 6 different inputs to only 5 different outputs without at least two inputs sharing the same output.
Examples of Injective Functions
Let's look at some examples using graphs and equations. When we talk about f(x):ℝ→ℝ, it means both the input (x) and the output (f(x)) are real numbers (all the numbers on the number line, including decimals and fractions).
Checking for Injections with Graphs
- Graphic meaning: You can tell if a function is injective by looking at its graph. If every horizontal line you draw crosses the graph in at most one point, then the function is injective. If a horizontal line crosses the graph more than once, it's not injective.
Checking for Injections with Algebra
- Algebraic meaning: A function f is injective if whenever f(x0) equals f(x1), it means that x0 must be equal to x1.
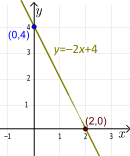
Straight Lines
Example: A linear function like y = ax + b (where a is not zero) is always an injection.
- Think about it: a straight line that isn't flat will only ever be crossed once by any horizontal line.
- Let's prove it: Suppose we have two different inputs, x0 and x1, that give the same output: a⋅x0 + b = a⋅x1 + b.
- If we subtract b from both sides, we get a⋅x0 = a⋅x1.
- Since a is not zero, we can divide both sides by a, which gives us x0 = x1.
- This shows that if the outputs are the same, the inputs must have been the same. So, it's an injection!
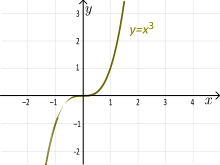
Cubic Functions
Example: The function f(x) = x3 is an injection.
- If you graph y = x3, any horizontal line will cross it only once.
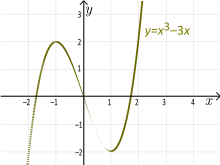
Example: But the function f(x) = x3 – 3x is not an injection.
- If you graph this, you'll see that some horizontal lines (like those between y = -2 and y = 2) will cross the graph three times. This means three different x-values give the same y-value, so it's not injective.
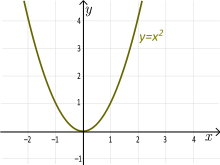
Quadratic Functions
Example: The quadratic function f(x) = x2 is not an injection.
- Think about it: f(2) = 22 = 4, and f(-2) = (-2)2 = 4.
- Here, two different inputs (2 and -2) give the same output (4).
- On a graph, any horizontal line above the x-axis will cross the parabola in two places.
Tip: You can sometimes make a function injective by restricting its domain. This means you only allow certain inputs.
- For example, if we only allow x to be zero or positive numbers for f(x) = x2, then f(x) = x2 becomes an injection. This is because we've removed all the negative x values that caused the problem.
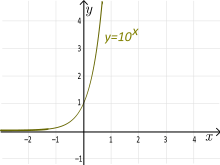
Exponential Functions
Example: The exponential function f(x) = 10x is an injection.
- If you graph this, any horizontal line will cross it at most once. Lines above the x-axis cross it once, and lines on or below the x-axis don't cross it at all.
- This property is useful in calculations: if 10x0 = 10x1, then you know x0 must equal x1.
- For instance, if 100 = 10x-3, we know 100 is 102. So, 2 = x-3, which means x = 5.
| Injection: no horizontal line intersects more than one point of the graph | ||
Other Examples
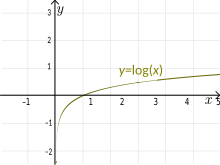
Example: The logarithmic function f(x) = log(x) (base 10) is an injection.
- This function is the opposite (or inverse) of 10x. Just like 10x, it passes the horizontal line test.
Example: Consider a function that takes any natural number (like 1, 2, 3, ...) and maps it to "2 times that number." So, 1 goes to 2, 2 goes to 4, 3 goes to 6, and so on.
- This function is an injection. Every even number has exactly one natural number that points to it (its pre-image). For example, 4 has only 2 pointing to it.
- Odd numbers don't have any natural number pointing to them in this function.
Related pages
See also
 In Spanish: Función inyectiva para niños
In Spanish: Función inyectiva para niños