Theorema egregium facts for kids
Theorema Egregium is a fancy Latin name that means "Remarkable Theorem." It's a very important idea in a part of math called differential geometry, which studies shapes and surfaces. A famous mathematician named Carl Friedrich Gauss proved this theorem.
This theorem is all about how surfaces curve. Imagine you have a piece of paper. You can bend it, roll it into a cylinder, or even twist it, but you're not stretching or tearing it. Gauss's theorem says that the "inner" curvature of that paper, called its Gaussian curvature, stays exactly the same no matter how you bend it, as long as you don't stretch it.
What makes it "remarkable" is that the usual way to define this curvature seems to depend on how the surface sits in 3D space. But Gauss showed that you can figure out this curvature just by measuring things on the surface itself, like angles and distances. You don't need to know anything about the space around it!
Contents
What is Curvature?
Curvature is a way to describe how much a surface bends. Think about a flat table. It has no curvature. Now think about a ball. It curves a lot in every direction. A cylinder, like a soda can, curves in one direction (around the can) but is flat in another (along its length).
Measuring Curvature
Mathematicians use special ways to measure curvature. For surfaces, one important measure is called Gaussian curvature. It tells you how much a surface curves at a specific point. If you imagine a tiny circle on a surface, how that circle changes when you move it around helps define its Gaussian curvature.
Gauss's Big Idea
Gauss's theorem says that if you have a surface, like a piece of rubber, and you bend it without stretching or shrinking any part of it, its Gaussian curvature won't change. This is super important because it means this type of curvature is a property of the surface itself, not just how it's placed in space.
Why is it Remarkable?
It's remarkable because when mathematicians first thought about curvature, they usually thought about how a surface curves in the space around it. For example, how a sphere curves when it's sitting in our normal 3D world. Gauss's theorem showed that even if you bend and twist a surface, as long as you don't stretch it, its "inner" curvature stays the same. It's like the surface has its own built-in curvature that doesn't depend on outside forces.
Real-World Examples
This theorem has many cool uses and helps us understand the world around us.
Maps and the Earth
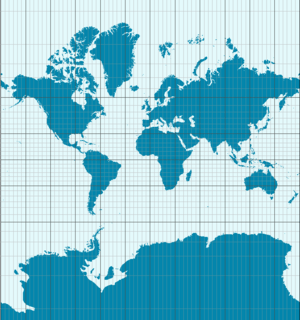
One great example of Theorema Egregium in action is making maps of the Earth. The Earth's surface is curved. If you try to flatten it onto a 2D map, you have to stretch or shrink some parts. This is why no flat map can perfectly show the Earth without some distortion. The Mercator projection, for instance, makes areas near the poles look much bigger than they are in reality. This is a direct result of Gauss's theorem – you can't flatten a curved surface without changing its "inner" measurements.
Bending Surfaces
Imagine you have a sheet of paper. You can roll it into a cylinder or cone. When you do this, you're bending the paper, but you're not stretching or tearing it. According to Gauss's theorem, the Gaussian curvature of the paper remains zero everywhere, just as it was when it was flat. This is why you can't make a perfect sphere out of a flat piece of paper without crumpling or cutting it – a sphere has positive Gaussian curvature, and a flat piece of paper has zero.
Images for kids
-
This animation shows a helicoid (like a spiral ramp) changing into a catenoid (like a soap film between two rings). This happens by bending the surface without stretching it. Notice how the shape changes, but the Gaussian curvature at each point stays the same.
See also
In Spanish: Theorema egregium para niños
