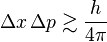Uncertainty principle facts for kids
The Uncertainty Principle is also known as the Heisenberg Uncertainty Principle. It's a big secret of the universe that Werner Heisenberg discovered. It means that tiny things, like electrons, don't have a perfectly clear position (where they are) or a perfectly clear momentum (how fast they're going and in what direction) at the same time.
Imagine trying to find a tiny, super-fast particle. If you try really hard to figure out its exact position, you'll lose track of its speed and direction. And if you try to know its speed and direction perfectly, you won't know its exact position. It's like trying to catch a slippery fish – the more you squeeze to hold it, the more it might slip away!
In our everyday lives, we can easily measure where a car is and how fast it's going. That's because the tiny uncertainties are too small for us to notice. We assume the car's path won't change if we just mark its spot. But for super-small things like electrons, it's different. When we try to measure an electron's position, our measurement actually changes its momentum. It's not that we're bad at measuring; it's just how the universe works at that tiny level.
This strange idea has led to amazing discoveries. For example, it helps us understand nuclear fission, which gives us a lot of energy. It also explains quantum tunneling, which is how some parts of computers work!
When scientists talk about this, they often use the words "position" and "momentum." Momentum is a mix of how fast something is moving and its direction. Sometimes it's easier to think about the "path" or "trajectory" something follows, which includes both speed and direction.
Contents
Seeing Uncertainty in Action
Here are some pictures to help you understand the Uncertainty Principle better:
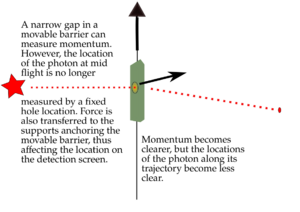
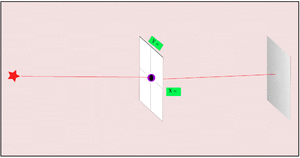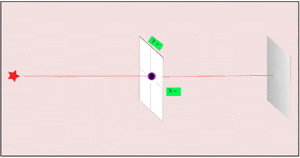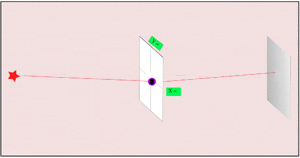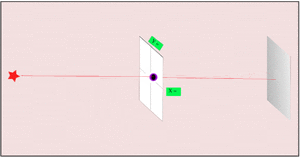
2. If we make the hole smaller, the particles' paths bend around the edges. This is called diffraction. It makes the beam of particles spread out more.
|
3. Making the hole smaller means we know the particle's position more exactly when it passes through. But then, its direction after the hole becomes much less certain. The spot where it lands gets blurry. If the hole is wide, we know its direction better, but not its exact position when it went through.
|
|
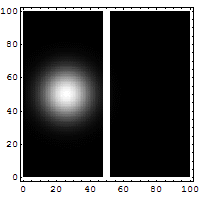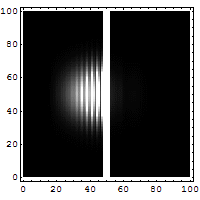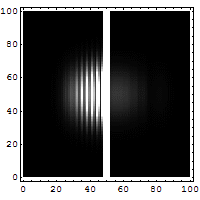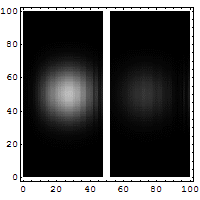
6. This animation shows quantum tunneling. It's a strange effect where a tiny particle can sometimes pass through a barrier, even if it doesn't have enough energy to go over it. This happens because of the Uncertainty Principle.
|
How Scientists Discovered Uncertainty
Werner Heisenberg came up with a new way to understand physics for very small things. From his math, he found something unexpected:
This math formula basically says:
- The amount of uncertainty in a particle's position (Δx) multiplied by the amount of uncertainty in its momentum (Δp) is always greater than or equal to a very tiny number (the Planck constant divided by 4π).
This means you can't be perfectly sure about both where something is and where it's going at the same time. If you get a super clear idea of its position, your idea of its momentum becomes less clear. And if you get a super clear idea of its momentum, your idea of its position becomes less clear.
Scientists already knew why some materials glow with specific colors when heated. Heisenberg was trying to figure out why these colors had different brightness levels. He didn't expect to find a fundamental secret of nature! He was just trying to explain why the colors of light from a hydrogen lamp, for example, weren't all equally bright.
Heisenberg's math was very complicated. He was trying to calculate the "intensity" (brightness) of light. He found a new way to do this, and it involved multiplying certain quantities in a very specific order.
Heisenberg noticed something strange: when he multiplied "position" by "momentum," he got a slightly different answer than when he multiplied "momentum" by "position." In everyday math with simple numbers, the order doesn't matter (2 x 3 is the same as 3 x 2). But with these quantum quantities, it did! This tiny difference was a huge discovery.
Heisenberg was tired, so he gave his work to his supervisor, Max Born. Born was a brilliant mathematician. He quickly realized that Heisenberg's equations were like a "recipe" for something called a "matrix" (a grid of numbers). Born knew that when you multiply matrices, the order often matters. He saw that the difference in results was always a tiny amount related to a special number called h/2πi. This difference is so small we can't see it in our daily lives.
Understanding the Uncertainty Principle
A couple of years later, Heisenberg proved the Uncertainty Principle, which is often written as Δx × Δp ≥ h/2. This number comes from his earlier work and shows the basic limit to how precisely we can know both position and momentum.
The letter h stands for the Planck constant. It's a tiny, mysterious number (about 6.62607 × 10^-34 joule seconds). It shows up a lot in quantum physics. It was discovered when scientist Max Planck realized that energy is released in tiny packets called "quanta."
The Uncertainty Principle tells us that when we try to measure certain pairs of things, we can only get so accurate. If we try to make one measurement super precise (like knowing position very well), the other measurement (like momentum) will become less precise. The amount of this "fuzziness" is connected to the Planck constant.
Another pair of things that follow this rule is energy (ΔE) and time (Δt): ΔE × Δt ≥ h. This means that for a very short time, a tiny amount of energy can pop into existence, even in empty space!
So, why is there this uncertainty? Scientists like Niels Bohr and his friends argued that tiny particles like photons and electrons don't actually have a definite position or momentum until we measure them. When we measure them, we interact with them, and that interaction forces them to "choose" a position or momentum within the limits of the Uncertainty Principle.
Imagine trying to find a ship at sea in the dark. You'd use a searchlight. The light wouldn't affect the ship's movement. But to find an electron with light, you'd have to hit it with photons. These photons would have enough energy to push the electron, changing its position and direction!
It's like trying to weigh something on a wobbly scale. You can try to make the scale steady, but at the super tiny level, things are always a bit "jiggly." We can't get perfect certainty because there's nothing perfectly definite to begin with.
Some scientists, like Albert Einstein, didn't like this idea. He believed that particles *did* have definite positions and momentums before being measured. He thought we just couldn't see them. But later experiments, based on ideas from John Stewart Bell, showed that nature really does behave in this uncertain way.
Another Way to Think About Uncertainty
Scientists also found that everything, not just light, has both a wave-like nature and a particle-like nature. This is called wave-particle duality.
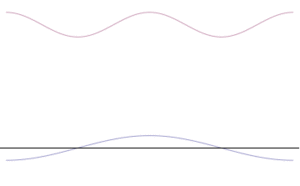
Imagine a wave that describes a particle. If you make this wave very narrow and tall, it means you know the particle's position very well. But to make it narrow, you have to combine many different waves with different wavelengths. Each wavelength relates to a different momentum. So, if you know the position well, you have many possible momentums, making the momentum uncertain.
On the other hand, if you want to know the momentum very precisely, you'd have a simple, long, pure wave. This wave would be spread out everywhere, meaning you wouldn't know the particle's exact position.
So, whether you think of particles as tiny balls or as waves, the Uncertainty Principle still applies. You can make one thing (position or momentum) more definite, but only by making the other less definite.
How Uncertainty Affects Our World
The Heisenberg Uncertainty Principle has changed how people think about many things, even free will.
In older physics, people thought that if you knew everything about the universe at one moment, you could predict everything that would happen next. This would mean that every choice we make is already decided. But the Uncertainty Principle suggests that things at the tiny level are not perfectly predictable. Instead, there are probabilities. This gives some people a reason to believe in free will, saying that our choices aren't completely set in stone.
You might have heard the phrases "quantum leap" or "quantum jump." People often use them to mean a huge, sudden change. But in physics, a quantum jump is actually a very tiny, sudden change. It's when an electron instantly moves from one energy level to another around an atom's nucleus, without passing through the space in between.
The Uncertainty Principle also shows how our actions can influence what we measure. When scientists try to measure a particle's location, it changes its momentum. This is a real effect of quantum physics. However, not all "observer effects" (where watching something changes it) are due to quantum uncertainty. For example, if a scientist studies a group of people, their presence might change how those people act. That's an observer effect, but it's not because of the Uncertainty Principle.
Sometimes, the word "quantum" is used in advertising to make something sound new and powerful. For example, some lawnmower engines are called "Quantum" engines!
Images for kids
-
This animation shows how a particle's wave spreads out over time. If you know its position well at the start, its momentum is uncertain, and its position becomes more uncertain later.
-
This shows how the probability of finding a particle spreads out over time if its momentum is very certain.
-
Werner Heisenberg (left) and Niels Bohr (right), two important scientists who helped us understand quantum physics.
See also
In Spanish: Relación de indeterminación de Heisenberg para niños
