Weighted arithmetic mean facts for kids

The weighted average (also called the weighted arithmetic mean) is a special kind of average. It's like a regular average, but some numbers in the group are more important than others. These "more important" numbers are given a higher "weight." Imagine you have different items, and some count more towards the total than others.

If all the numbers have the same importance (or "weight"), then the weighted average is exactly the same as a normal arithmetic mean. Weighted averages are used in many areas, especially in statistics, to get a more accurate picture when some data points matter more.

How Does a Weighted Average Work?

School Grades Example

Let's say there are two school classes. One class has 20 students, and the other has 30 students. They both took the same test.

• Morning class* (20 students): Their average test score was 80.
• Afternoon class* (30 students): Their average test score was 90.

If you just take the average of the two class averages (80 + 90) / 2 = 85, that's not quite right. Why? Because the classes have different numbers of students! The afternoon class has more students, so its average score should count more.

To find the true average score for all students, you need to use a weighted average:

• Multiply the morning class average by its number of students: 20 students × 80 = 1600
• Multiply the afternoon class average by its number of students: 30 students × 90 = 2700
• Add these results together: 1600 + 2700 = 4300
• Divide by the total number of students: 4300 / (20 + 30) = 4300 / 50 = 86.

So, the weighted average student grade is 86. This shows that the larger class has a bigger "weight" on the overall average.

Using Percentages (Convex Combination)

You can also think of weights as percentages. In our example, the total number of students is 50.

• The morning class has 20 out of 50 students: 20 / 50 = 0.4 (or 40%)
• The afternoon class has 30 out of 50 students: 30 / 50 = 0.6 (or 60%)

Now, apply these percentages (weights) to the class averages:

• (0.4 × 80) + (0.6 × 90) = 32 + 54 = 86.

This gives you the same weighted average of 86. This way of using weights that add up to 1 (like percentages) is called a convex combination.

The Math Behind It

The idea of a weighted average can be written as a formula. Imagine you have a list of numbers, like test scores, and each number has its own "weight."

Let's say your numbers are 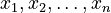Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x_1, x_2, \dots , x_n . And their corresponding weights are Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): w_1, w_2, \dots , w_n .

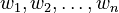The formula for the weighted average (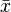) is: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle \bar{x} = \frac{ (w_1 \times x_1) + (w_2 \times x_2) + \cdots + (w_n \times x_n) }{ w_1 + w_2 + \cdots + w_n }}

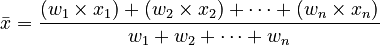
In simpler words:

• Multiply each number by its weight.
• Add all those results together.
• Divide that total by the sum of all the weights.

Numbers with a higher weight will have a bigger impact on the final weighted average. The weights must be positive numbers. They can be zero, but not all of them can be zero, because you can't divide by zero.

If all the weights are exactly the same, then the weighted average becomes just a regular arithmetic mean.

Weighted Variance

When you calculate an average, it's often helpful to know how spread out the numbers are around that average. This is called the variance. When you use a weighted average, the way you calculate the variance also changes.

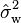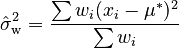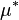The biased weighted sample variance () is found using this formula: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle \hat \sigma^2_\mathrm{w} = \frac{\sum w_i (x_i - \mu^{*})^2 }{\sum w_i}} Here, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mu^{*} is your weighted average. This formula helps you understand how much the individual numbers differ from the weighted average, taking their importance (weights) into account.

For smaller groups of numbers, there's a slightly different formula to make the variance estimate more accurate. This is similar to how a "Bessel's correction" is used for regular averages.

See also

In Spanish: Media ponderada para niños