Wheat and chessboard problem facts for kids

By the time you reach the fifth square on the chessboard, there are 31 grains of wheat in total. This is .

The wheat and chessboard problem is a famous math puzzle. It asks:

Imagine a chessboard. What if you put wheat grains on each square? You start with one grain on the first square. Then you put two grains on the second square. On the third square, you put four grains. You keep doubling the number of grains for each new square. How many grains of wheat would be on the chessboard when you finish?

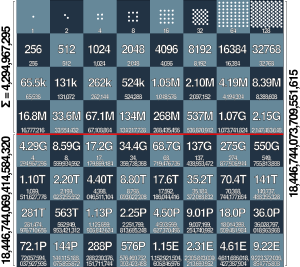
This problem can be solved using simple addition. A chessboard has 64 squares. If the number of grains doubles on each square, the total number of grains is 1 + 2 + 4 + 8 + ... and so on for all 64 squares.

The total number of grains turns out to be a huge number: 2⁶⁴-1. This is 18,446,744,073,709,551,615 grains! That's over 18 quintillion grains. To give you an idea, this is more than 2,000 times the amount of wheat the whole world produces in a year.

This problem helps show how quickly things grow when they double. It's a great way to learn about exponents and geometric series. You can also use it to understand things like compound interest. For example, if you had a penny that doubled every day for 30 days, you'd have over 10 million dollars by the end!

Story of the Chessboard Problem

This problem often appears in stories about how the game of chess was invented. One popular story tells of an ancient Indian minister named Sessa. He invented chess and showed it to his ruler.

The ruler was very impressed and offered Sessa any reward he wished. Sessa asked for wheat grains based on the chessboard problem. He asked for one grain on the first square, two on the second, four on the third, and so on.

The ruler laughed, thinking it was a very small prize for such a brilliant invention. But when his treasurers calculated the amount, they were shocked. The number of wheat grains was so huge it would be more than the ruler's entire kingdom could produce! Some stories say the inventor became a wise advisor, while others have a different ending.

Historians like Macdonnell have looked into the older versions of this story. They found that the idea of calculating huge numbers with a chessboard was known in ancient India. The Arabic word for a chessboard square, "beit," means "house." This might be linked to the Indian word "koṣṭhāgāra," which means "store-house" or "granary."

How to Solve the Problem

The total of powers of two (like 1, 2, 4, 8...) up to a certain number is always one less than the next power of two.

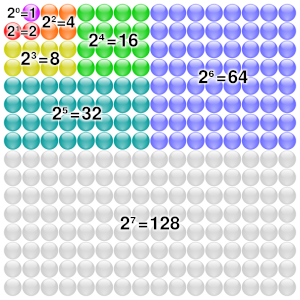
The simplest way to understand the solution is to just keep doubling and adding:

• Square 1: 1 grain
• Square 2: 2 grains
• Square 3: 4 grains
• Square 4: 8 grains

...and so on, all the way to the 64th square.

The total number of grains on the 64th square alone would be 2⁶³. The total number of grains on the entire board is 1 + 2 + 4 + ... + 2⁶³.

There's a neat trick to solve this quickly. The sum of all the grains is simply 2⁶⁴ - 1. Let's see why: Imagine the total sum is 's'. s = 1 + 2 + 4 + ... + 2⁶³ If you multiply 's' by 2: 2s = 2 + 4 + 8 + ... + 2⁶³ + 2⁶⁴ Now, if you subtract the first 's' from '2s': 2s - s = (2 + 4 + ... + 2⁶⁴) - (1 + 2 + ... + 2⁶³) Most of the numbers cancel out, leaving: s = 2⁶⁴ - 1

This problem is a great example of how exponents work and how quickly numbers can grow in an exponential or geometric pattern. Each square's number of grains is a power of 2: 2⁰ (for the first square), 2¹ (for the second), 2² (for the third), and so on, up to 2⁶³ for the last square.

The Second Half of the Chessboard

This picture shows the "second half of the chessboard" idea. The letters are short forms for very large numbers in the metric system.

In the world of technology, there's a saying called the "second half of the chessboard." This idea was made popular by Ray Kurzweil. It refers to the point where something that is growing very quickly (exponentially) starts to have a huge impact.

Let's look at the numbers for the chessboard:

• The first half of the chessboard has 32 squares. The total grains on these squares would be 2³² - 1, which is about 4.3 billion grains. This would weigh about 279 tonnes of wheat. That's a lot, but it's still manageable.

• Now, look at the second half of the chessboard (squares 33 to 64). The number of grains here is much, much larger. The first square of the second half (square 33) alone has 2³² grains, which is more than all the grains on the entire first half!

• On the 64th square alone, there would be 2⁶³ grains. That's over 9 quintillion grains! This is more than two billion times the amount on the first half of the chessboard.

• The total for the entire chessboard is 2⁶⁴ - 1 grains. This huge amount of wheat would weigh about 1.2 billion metric tons. To compare, this is about 1,645 times more than all the wheat produced globally in 2014. This shows how incredibly fast exponential growth can become.

Why This Problem Matters

The wheat and chessboard problem is often used to explain how things can grow very quickly. Carl Sagan, a famous scientist, wrote about this in his book. He explained that things that grow exponentially can't keep going forever. They will eventually use up all available resources.

This idea is also used in a famous book called The Limits to Growth. It uses the chessboard story to show what might happen if things like population or resource use keep growing exponentially without limits. It teaches us that in a world with limited space and resources, exponential growth cannot continue forever.

See also

In Spanish: Problema del trigo y del tablero de ajedrez para niños