Exponential growth facts for kids

The graph shows how exponential growth (green) quickly becomes much bigger than linear (red) or cubic (blue) growth.      Linear growth      Cubic growth      Exponential growth

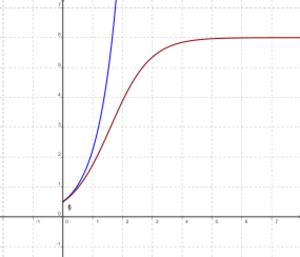
Exponential growth is a way that something can increase over time. It means that the amount growing gets bigger and bigger, faster and faster. Imagine a snowball rolling down a hill: it picks up more snow as it goes, so it gets bigger, and then it picks up even more snow because it's bigger. That's a bit like exponential growth!

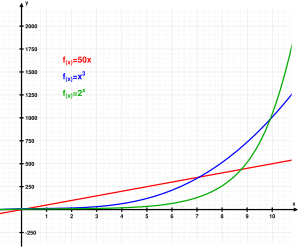
This type of growth happens when the speed at which something changes is directly related to how much of it there already is. For example, if you have a small amount, it grows slowly. But as it gets larger, it grows much faster. When something grows exponentially, its value can be described by an exponential function. This is different from other types of growth, like quadratic growth, where the increase is not as dramatic.

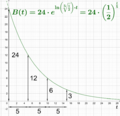
If the number describing the growth is negative, then the quantity shrinks over time. This is called exponential decay. When we look at growth in steps (like every hour or every day), it's also called geometric growth or geometric decay. This is because the numbers form a geometric progression, where each number is found by multiplying the previous one by a fixed number.

A simple way to show exponential growth is with this formula: 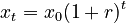Here, x₀ is the starting amount, r is the growth rate (how fast it's growing), and t is the time that has passed.

Think about a colony of bacteria. One bacterium splits into two. Then those two split into four. Those four split into eight, and so on. The number of new bacteria keeps increasing because it depends on the ever-growing number of bacteria already there. You can see this kind of growth in real life, like how a virus spreads, how compound interest makes debt grow, or how viral videos become popular.

However, real-life exponential growth usually doesn't last forever. Eventually, things slow down because of limits, like not enough food for bacteria or space for people. This often turns into what's called logistic growth.

Sometimes, people think "exponential growth" just means "really fast growth." But something growing exponentially can actually start very slowly. It's the way the growth speeds up over time that makes it exponential.

Examples of Exponential Growth

Bacteria grow exponentially when they have everything they need.

In Biology

• Microorganisms: The number of microorganisms in a culture (like bacteria in a dish) will grow exponentially. This continues until they run out of an important nutrient. One organism splits into two, then those two split to make four, and so on.
• Viruses: A virus (like COVID-19) often spreads exponentially at first, especially if people don't have immunity. Each infected person can infect several new people, causing the numbers to rise very quickly.

In Physics

• Nuclear Chain Reactions: This is the idea behind nuclear reactors and nuclear weapons. When a uranium atom splits, it releases particles called neutrons. Each of these neutrons can then cause other uranium atoms to split. If enough neutrons are absorbed by other atoms, the number of splitting atoms grows exponentially, leading to a huge release of energy.

In Money and Business

• Compound Interest: When you earn compound interest on savings, your money grows exponentially. You earn interest not just on your original money, but also on the interest you've already earned. This makes your money grow faster over time.
• Pyramid Schemes: These are illegal schemes where early investors make money by getting new investors to join. The number of people needed grows exponentially, meaning it quickly becomes impossible to find enough new people, and most people lose money.

In Computers

• Computer Power: The processing power of computers has grown exponentially for many years, following something called Moore's law. This means computers get twice as powerful about every two years.
• Complex Algorithms: In computer science, some computer programs (called algorithms) need an exponentially increasing amount of time or memory as the problem they are solving gets a little bit bigger. This means these programs quickly become too slow or use too much memory for even slightly larger problems.

On the Internet

• Viral Content: Things like internet memes or viral videos can spread exponentially. On social networks, one person can share content with many friends, who then share it with even more people. This causes the content to spread very rapidly. For example, the music video "Gangnam Style" was watched by millions in just a few weeks.

How Exponential Growth Works (Basic Formula)

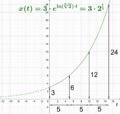
A quantity x grows exponentially over time t if it follows this pattern: 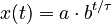Here:

• a is the starting amount of x (at time 0).
• b is a positive number that shows how much it grows each time period.
• τ (tau) is the time it takes for x to grow by one factor of b.

If τ is positive and b is greater than 1, then you have exponential growth. If b is between 0 and 1 (like 0.5), or if τ is negative, then you have exponential decay (the quantity shrinks).

Example: If a type of bacteria doubles every ten minutes, and you start with just one bacterium, how many would there be after one hour? Here, the starting amount , the growth factor (because it doubles), and the time for one growth period . We want to know how many after 1 hour, which is 60 minutes. 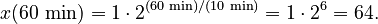Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle x(60\text{ min}) = 1 \cdot 2^{(60\text{ min})/(10\text{ min})} = 1 \cdot 2^6 = 64.} So, after one hour, there would be 64 bacteria!

Other ways to write the exponential growth formula use different numbers as the base, but they all mean the same thing: 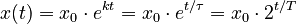Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle x(t) = x_0\cdot e^{kt} = x_0\cdot e^{t/\tau} = x_0 \cdot 2^{t/T}}

• x₀ is the initial amount.
• k is the growth constant.
• τ is the e-folding time (time to grow by a factor of e, which is about 2.718).
• T is the doubling time (time it takes to double).

A quick way to estimate the doubling time is the rule of 70: divide 70 by the percentage growth rate. For example, if something grows by 10% per year, it will double in about 7 years (70/10 = 7).

When Growth Stops Being Exponential

The J-shaped exponential growth (left, blue) and the S-shaped logistic growth (right, red).

In the real world, things don't usually grow exponentially forever. After a while, outside factors or the environment slow them down. For example, a population might hit an upper limit because there isn't enough food or space. In 1845, a Belgian mathematician named Pierre François Verhulst created a model for this kind of growth, called "logistic growth". It shows growth slowing down and leveling off.

Understanding Exponential Growth Can Be Tricky

Studies show that people often find it hard to truly understand how fast exponential growth can become. This can lead to mistakes, especially with money.

The Rice on a Chessboard Story

There's a famous legend about a king and a wise man. The king offered the wise man any reward for a gift. The wise man asked for one grain of rice on the first square of a chessboard, two grains on the second, four on the third, and so on, doubling the rice for each square. The king thought this was a small request.

At first, it seemed easy. But by the 21st square, it was over a million grains. By the 41st square, it was more than a trillion grains! There wasn't enough rice in the entire world to fill the last squares. This story shows how quickly numbers can grow when they double repeatedly.

The Water Lily Riddle

Here's a riddle often told to children: A water lily plant in a pond doubles in size every day. If left alone, it would cover the whole pond in 30 days and kill all other life. The plant's growth seems small for a long time, so people decide not to worry until it covers half the pond. Which day will that be?

The answer is the 29th day! This leaves only one day to save the pond. This riddle shows how quickly an exponentially growing thing can reach its limit, often seeming to happen suddenly at the very end.

Images for kids

• 

  exponential growth

• 

  exponential decay

• 

  Graphs comparing doubling times and half lives of exponential growths (bold lines) and decay (faint lines), and their 70/t and 72/t approximations.