Bhāskara I facts for kids
Quick facts for kids
Bhāskara I
|
|
|---|---|
| Born | c. 600 CE |
| Died | c. 680 CE |
| Nationality | Indian |
| Occupation | Mathematician; scientist |
| Known for | Bhaskara I's sine approximation formula |
Bhāskara (around 600–680 CE), often called Bhaskara I, was an important Indian mathematician and astronomer from the 7th century. He is famous for being one of the first to write numbers using the Hindu decimal system. This system used a small circle to represent zero, just like we do today!
Bhaskara also found a very clever way to estimate the value of the sine function. He wrote a special book called Āryabhaṭīyabhāṣya in 629 CE. This book was a commentary on the work of another famous mathematician, Aryabhata. It is one of the oldest known books in Sanskrit about mathematics and astronomy. He also wrote two other books on astronomy: the Mahābhāskarīya and the Laghubhāskarīya.
To honor his work, the Indian Space Research Organisation launched a satellite named Bhaskara I on June 7, 1979.
Contents
Bhaskara's Life Story
We don't know a lot about Bhaskara's personal life. He was likely an astronomer and was born in India during the 7th century. In his writings, he mentioned several places in India. For example, he talked about Vallabhi (now called Vala) and Sivarajapura, which were in a region called Saurashtra. Today, Saurashtra is part of the Gujarat state on India's west coast. He also mentioned Bharuch in southern Gujarat and Thanesar in eastern Punjab.
It's thought that Bhaskara was born in Saurashtra and later moved to Asmaka. His father taught him about astronomy. Bhaskara is considered one of the most important scholars who followed Aryabhata's ideas about astronomy. He and another famous mathematician named Brahmagupta made big contributions to understanding fractions.
How Bhaskara Showed Numbers
Perhaps Bhaskara's most important math contribution was how he showed numbers using a positional system. This means the position of a digit in a number gives it a specific value (like how the '2' in 20 is different from the '2' in 200).
Before Bhaskara, Indian astronomers had used positional systems for about 500 years. However, they didn't use figures or symbols. Instead, they wrote numbers using words or stories, often in poems! For example, the number 1 might be called "moon" because there's only one moon. The number 2 might be "wings" or "eyes" because they come in pairs. The number 5 could be "senses." These words were put together so that each word's position showed its power of ten, but in reverse order compared to how we write numbers today.
Bhaskara's system was truly positional because the same words could mean 40 or 400, depending on their place. What's really amazing is that he often explained numbers written in this word system by also writing them with the first nine Brahmi numerals. He used a small circle for zero. Unlike his word system, he wrote these figures from left to right, with the largest values first, exactly like we do today!
So, by at least 629 CE, the decimal system was definitely known to Indian scientists. Bhaskara probably didn't invent it, but he was the first to use these Brahmi numerals in his scientific writings in Sanskrit without any hesitation.
Other Important Discoveries
Mathematics
Bhaskara wrote three important books about astronomy that included a lot of mathematics. In 629 CE, he wrote notes on the Aryabhatiya, which was a book of poems about mathematical astronomy. His notes focused on 33 verses that dealt with math, including equations and trigonometric formulas.
His book Mahabhaskariya has eight chapters about mathematical astronomy. In chapter 7, he shared a remarkable formula to estimate the sine of an angle. This formula is: 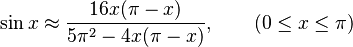 He said that Aryabhata had discovered this formula. It's very accurate, with an error of less than 1.9%. Bhaskara also explained how sine and cosine are related. He showed how to find the sine of angles larger than 90°, 180°, or 270° by relating them to angles smaller than 90°. Parts of Mahabhaskariya were later translated into Arabic.
He said that Aryabhata had discovered this formula. It's very accurate, with an error of less than 1.9%. Bhaskara also explained how sine and cosine are related. He showed how to find the sine of angles larger than 90°, 180°, or 270° by relating them to angles smaller than 90°. Parts of Mahabhaskariya were later translated into Arabic.
Bhaskara also worked on a math idea that if p is a prime number, then 1 + (p–1)! can be divided by p. This idea was later proven by Alhazen and is now known as Wilson's theorem.
He also discussed how to solve certain equations called Pell equations. For example, he asked: "Tell me, O mathematician, what is that square which multiplied by 8 becomes - together with unity - a square?" In simpler terms, he was asking for solutions to the equation 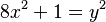 . One easy solution is x = 1, y = 3. From this, other solutions can be found, like (x,y) = (6,17).
. One easy solution is x = 1, y = 3. From this, other solutions can be found, like (x,y) = (6,17).
Astronomy
The Mahabhaskariya book has eight chapters that cover many topics in mathematical astronomy. These include:
- The positions of the planets.
- How planets relate to each other and to bright stars.
- The shape of the lunar crescent (the moon's visible part).
- Solar and lunar eclipses.
- When planets rise and set in the sky.
See also
 In Spanish: Bhaskara I para niños
In Spanish: Bhaskara I para niños

