Divide-and-conquer algorithm facts for kids
In computer science, divide and conquer is a smart way to solve problems. It's like breaking a huge task into smaller, easier pieces. An algorithm using this method keeps splitting a problem into two or more smaller parts. This continues until the parts are simple enough to solve easily. Then, the solutions to these small parts are put back together. This gives you the answer to the original big problem.
This technique helps create very fast computer programs. It's used for things like sorting lists (like quicksort and merge sort). It also helps multiply huge numbers quickly (like the Karatsuba algorithm). Other uses include finding the closest two points in a group. It's also key for understanding computer languages (syntactic analysis) and for FFT, which is used in signal processing.
Making these algorithms can be tricky. Sometimes, you need to think about the problem in a new way to make it fit this method. We often use mathematical induction to prove that a divide-and-conquer algorithm works correctly.
Contents
What is Divide and Conquer?
The "divide and conquer" idea helps find the best way to solve a problem. The main goal is to break a problem into smaller, similar parts. You solve each small part, then combine their answers to solve the main problem. If a part is super simple, you just solve it right away.
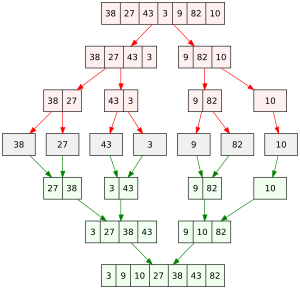
For example, imagine you have a long list of numbers to sort. You could split it into two shorter lists. Then, you sort each of those shorter lists. Finally, you combine the two sorted lists into one big sorted list. This method is called merge sort.
Sometimes, people use "divide and conquer" for algorithms that only make one smaller problem. An example is binary search. This algorithm finds an item in a sorted list by repeatedly cutting the search area in half. These types of algorithms can be very fast. Some experts prefer to call these "decrease and conquer" algorithms. They save the "divide and conquer" name for methods that create two or more sub-problems.
History of Divide and Conquer
Some early examples of these algorithms are "decrease and conquer" types. This means the problem is broken down into just one smaller problem at each step. These can often be solved by repeating steps in a loop.
The binary search method has been around for a long time. It cuts the problem size in half each time. A clear description for computers appeared in 1946. But the idea of using sorted lists to search goes back to ancient Babylonia around 200 BC! Another old "decrease and conquer" method is the Euclidean algorithm. It finds the greatest common divisor of two numbers. This algorithm is many centuries old.
An early "divide and conquer" example with multiple sub-problems is the Cooley–Tukey fast Fourier transform (FFT) algorithm. Carl Friedrich Gauss described it in 1805. However, it didn't become widely used until much later.
The merge sort algorithm is a key example for computers. John von Neumann invented it in 1945. It was one of the first two-sub-problem D&C algorithms designed for computers.
In 1960, Anatolii Alexeevitch Karatsuba created an amazing algorithm. It could multiply two large numbers much faster than thought possible. This showed that some problems could be solved quicker than expected.
Even outside computers, we see divide and conquer. Donald Knuth points out how a post office sorts mail. Letters are put into bags for different areas. Each bag is then sorted into smaller regions, and so on. This is like a radix sort method.
Why Use Divide and Conquer?
Solving Hard Problems
Divide and conquer is great for problems that seem very difficult. You just need a way to break the problem into smaller parts. You also need to know how to solve the simplest cases. And finally, you need a way to put the solutions back together.
Making Algorithms Faster
This method often leads to much faster algorithms. It was key to the quick multiplication method by Karatsuba. It also helped create the quicksort and mergesort algorithms. The Strassen algorithm for multiplying matrices and fast Fourier transforms also use this idea.
These D&C methods often make algorithms much more efficient. For example, if splitting and combining steps are fast, the total time can be much less.
Working with Multiple Processors
Divide-and-conquer algorithms are perfect for computers with many processors. Each processor can work on a different sub-problem at the same time. This makes the overall task finish much faster.
Better Memory Use
These algorithms also use computer memory efficiently. When a sub-problem becomes small enough, it can often be solved entirely within the computer's fast memory cache. This avoids needing to access the slower main memory. Algorithms designed this way are called cache-oblivious. They work well without needing to know the exact size of the cache. This same benefit applies to other types of memory storage too.
How Divide and Conquer is Used
Using Recursion
Divide-and-conquer algorithms are often written using recursive procedures. A recursive function is one that calls itself to solve smaller versions of the problem. The computer keeps track of the smaller problems using something called a call stack.
Choosing Simple Cases
In any recursive algorithm, you need to decide when to stop splitting. These are called base cases. They are the small problems that are solved directly.
Choosing the simplest possible base cases makes the program cleaner. For example, a quicksort algorithm could stop when a list has only one item. A list with one item is already sorted!
However, it's often faster to stop the recursion a bit earlier. You can solve slightly larger base cases without recursion. This creates a hybrid algorithm. It avoids the extra work of calling the function for very tiny problems. For instance, many quicksort programs switch to a simpler sorting method for very small lists.
Handling Repeated Problems
Sometimes, a divide-and-conquer algorithm might try to solve the same small problem many times. To avoid this, we can use a technique called memoization. This means saving the answers to problems you've already solved. If you need that answer again, you just look it up instead of re-calculating it. This idea leads to dynamic programming, which is a powerful way to solve complex problems.
See also
 In Spanish: Algoritmo divide y vencerás para niños
In Spanish: Algoritmo divide y vencerás para niños
- Akra–Bazzi method
- Decomposable aggregation function
- Fork–join model
- Master theorem (analysis of algorithms)
- Mathematical induction
- MapReduce
- Heuristic (computer science)
 | Janet Taylor Pickett |
 | Synthia Saint James |
 | Howardena Pindell |
 | Faith Ringgold |