Edward Nelson facts for kids

Quick facts for kids Edward Nelson
Edward Nelson
Born	(1932-05-04)May 4, 1932 Decatur, Georgia
Died	September 10, 2014(2014-09-10) (aged 82) Princeton, New Jersey
Citizenship	American
Alma mater	University of Chicago (MS, 1953) University of Chicago (PhD, 1955)
Known for	Internal set theory Stochastic quantum mechanics Stochastic quantization Hadwiger–Nelson problem Nelson's axioms
Spouse(s)	Nancy Wong Nelson Sarah Jones Nelson
Children	2
Awards	Leroy P. Steele Prize
Scientific career
Fields	Physics Mathematics
Institutions	Institute for Advanced Study Princeton University
Thesis	On the Operator Theory of Markoff Processes
Doctoral advisor	Irving Segal
Notable students	Eric Anders Carlen Richard M. Dudley John D. Lafferty Greg Lawler

Edward Nelson (May 4, 1932 – September 10, 2014) was an American mathematician. He was professor in the Mathematics Department at Princeton University. He was known for his work on mathematical physics and mathematical logic. In mathematical logic, he was noted especially for his internal set theory, and views on ultrafinitism and the consistency of arithmetic. In philosophy of mathematics he advocated the view of formalism rather than platonism or intuitionism. He also wrote on the relationship between religion and mathematics.

Biography

Edward Nelson was born in Decatur, Georgia, in 1932. He spent his early childhood in Rome where his father worked for the Italian YMCA. At the advent of World War II, Nelson moved with his mother to New York City, where he attended high school at the Bronx High School of Science. His father, who spoke fluent Russian, stayed in St. Petersburg in connection with issues related to prisoners of war. After the war, his family returned to Italy and he attended the Liceo Scientifico Giovanni Verga in Rome.

He received his Ph.D. in 1955 from the University of Chicago, where he worked with Irving Segal. He was a member of the Institute for Advanced Study from 1956 to 1959. He held a position at Princeton University starting in 1959, attaining the rank of professor there in 1964 and retiring in 2013.

In 2012 he became a fellow of the American Mathematical Society. He died in Princeton, New Jersey, on September 10, 2014.

Academic work

Stochastic quantum mechanics

Nelson made contributions to the theory of infinite-dimensional group representations, the mathematical treatment of quantum field theory, the use of stochastic processes in quantum mechanics, and the reformulation of probability theory in terms of non-standard analysis. For many years he worked on mathematical physics and probability theory, and he retained a residual interest in these fields, particularly in connection with possible extensions of stochastic mechanics to field theory.

Four color problem

In 1950, Nelson formulated a popular variant of the four color problem: What is the chromatic number, denoted 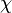, of the plane? In more detail, what is the smallest number of colors sufficient for coloring the points of the Euclidean plane such that no two points of the same color are unit distance apart? We know by simple arguments that 4 ≤ χ ≤ 7. The problem was introduced to a wide mathematical audience by Martin Gardner in his October 1960 Mathematical Games column. The chromatic number problem, also now known as the Hadwiger–Nelson problem, was a favorite of Paul Erdős, who mentioned it frequently in his problems lectures. In 2018, Aubrey de Grey showed that χ ≥ 5.

Foundations of mathematics

In the later part of his career, he worked on mathematical logic and the foundations of mathematics. One of his goals was to extend IST (Internal Set Theory—a version of a portion of Abraham Robinson's non-standard analysis) in a natural manner that includes external functions and sets, in a way that provides an external function with specified properties unless there is a finitary obstacle to its existence. Other work centered on fragments of arithmetic, studying the divide between those theories interpretable in Raphael Robinson's arithmetic and those that are not; computational complexity, including the problem of whether P is equal to NP or not; and automated proof checking.

In September 2011, Nelson announced that he had proved that Peano arithmetic was logically inconsistent. An error was found in the proof by Terence Tao, and Nelson retracted the claim.

See also