Group representation facts for kids

A representation of a group "acts" on an object. A simple example is how the symmetries of a regular polygon, consisting of reflections and rotations, transform the polygon.

In mathematics, group representations help us understand abstract groups. They do this by showing group elements as linear transformations. Think of these as special changes to a vector space, like rotations or reflections.

Basically, group representations let us turn tricky group problems into easier problems. These easier problems can be solved using linear algebra, which deals with things like matrices. This is very helpful in physics and chemistry. For example, they can explain how the symmetry of a molecule affects its behavior.

In a broader sense, a "representation" is any way to describe a group. It shows how a group acts on some mathematical object. If this object is a vector space, we call it a linear representation. This article mainly focuses on linear representations.

What are Group Representations?
- Important Terms
Examples of Group Representations
Reducibility of Representations
Generalizations of Representations
- Set-Theoretic Representations
- Representations in Other Categories
See also

What are Group Representations?

A representation of a group G is like a special map. This map takes each element from group G and turns it into a linear transformation. These transformations act on a vector space V.

Imagine you have a group of actions, like spinning a shape. A representation lets you describe each spin as a mathematical operation. This operation changes the coordinates of points in a space.

Here's how it works:

You have a group G.
You have a vector space V. Think of V as a space where you can add "vectors" (like arrows) and multiply them by numbers.
The representation is a function, often called ρ (rho). It takes an element g from group G. Then it gives you a transformation ρ(g) that acts on V.
This transformation must be a linear transformation. This means it keeps lines straight and doesn't move the origin (0,0).
Also, if you combine two group elements, say g₁ and g₂, their transformations must combine in the same way. So, ρ(g₁ g₂) must be the same as ρ(g₁) followed by ρ(g₂).

The vector space V is called the representation space. The number of dimensions of V is the dimension of the representation.

If V has a finite number of dimensions, we can use matrices to show these transformations. An n-by-n matrix can represent a transformation in an n-dimensional space.

Important Terms

Continuous representation: If the group G and the vector space V are "continuous" (like a smooth line or surface), then the representation must also be continuous. This means small changes in the group element lead to small changes in the transformation.
Kernel: The kernel of a representation ρ is the set of group elements that don't change anything in the vector space. They map to the "identity transformation" (which leaves everything as it is).
Faithful representation: A representation is faithful if its kernel contains only the group's identity element. This means every different group element creates a different transformation. It's like a perfect copy of the group.
Equivalent representations: Two representations are equivalent if they are essentially the same. They might look different (e.g., use different matrices), but you can transform one into the other using a simple change of coordinates.

Examples of Group Representations

Let's look at a simple example. Consider the cyclic group C₃. This group has three elements: 1, u, and u². Here, u is a special complex number that, when multiplied by itself three times, equals 1 (like a rotation by 120 degrees).

We can represent this group using 2x2 matrices.

For the element 1 (the identity), the matrix is:

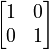Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} This matrix does nothing; it's the identity transformation.

For the element u, one possible matrix is:

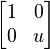
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix} 1 & 0 \\ 0 & u \\ \end{bmatrix}

For the element u², the matrix is:

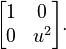
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix} 1 & 0 \\ 0 & u^2 \\ \end{bmatrix}.

This representation is faithful because each group element maps to a unique matrix.

Another way to represent C₃ is using rotations in a 2D space. If you imagine a triangle, the group C₃ describes rotating it by 0, 120, or 240 degrees. These rotations can be shown with matrices using real numbers.

For example, if u is the complex number -1/2 + i√3/2, then:

For the element u, the matrix is:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix} -1/2 & -\sqrt{3}/2 \\ \sqrt{3}/2 & -1/2 \\ \end{bmatrix} This matrix represents a 120-degree rotation.

For the element u², the matrix is:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix} -1/2 & \sqrt{3}/2 \\ -\sqrt{3}/2 & -1/2 \\ \end{bmatrix} This matrix represents a 240-degree rotation.

Reducibility of Representations

Imagine your representation space V is like a big room. A subrepresentation is like a smaller, special room inside V. This smaller room has the property that if you apply any transformation from the group, points that start in the smaller room will always stay in that smaller room.

A representation is irreducible if its only subrepresentations are the "zero-dimensional" space (just a single point) and the entire space V itself. It means you can't break it down into smaller, independent parts.
A representation is reducible if it has a proper subrepresentation that is not zero-dimensional. This means you can simplify it into smaller, independent representations.

For many groups, especially finite groups (groups with a limited number of elements) over complex numbers, representations can be broken down. They can be seen as a direct sum of several irreducible subrepresentations. This is like saying a complex machine can be understood by looking at its simpler, independent components.

In our C₃ example above, the first two representations (using complex numbers) are reducible. They can be split into two 1-dimensional parts. The third representation (using real numbers for rotations) is irreducible. You can't break down a rotation into simpler, independent actions in the same way.

Generalizations of Representations

Group representations can be thought of in even broader ways.

Set-Theoretic Representations

A set-theoretic representation (also called a group action or permutation representation) shows how a group G acts on a simple set X. Instead of transforming a vector space, the group elements just rearrange the items in the set.

For example, if X is a set of three balls, a group of permutations could describe how you can swap the positions of these balls. Each group element corresponds to a specific way of rearranging the balls.

Representations in Other Categories

In advanced mathematics, groups can be seen as simple "categories." A representation of a group in another "category" (like the category of topological spaces) means finding a way for the group to act on objects in that category.

For example:

If the category is about vector spaces, you get linear representations (what we've discussed).
If the category is about sets, you get set-theoretic representations.
If the category is about topological spaces, the group elements become transformations that preserve the "shape" or "connectedness" of the space.

Two types of representations related to linear ones are:

Projective representations: These are like linear representations but allow for some scaling.
Affine representations: These act on affine spaces, which are like vector spaces but without a fixed origin. The Euclidean group (rotations, reflections, and translations) acts affinely on Euclidean space.