Molecular symmetry facts for kids
Molecular symmetry is a cool idea in chemistry that helps us understand how molecules are shaped. It's all about how balanced and identical a molecule looks when you turn it or flip it. This helps scientists guess or explain many things about how a molecule acts.
Chemists use symmetry to figure out how crystals form and how chemical reactions happen. Knowing a molecule's symmetry can even help predict what new molecules will be made in a reaction and how much energy is needed for it to happen.
One of the main ways to study molecular symmetry is using something called Group theory. This idea is also helpful for understanding how molecular orbitals (the spaces where electrons hang out in a molecule) are arranged. Scientists find out about molecular symmetry using tools like X-ray crystallography and other ways of looking at molecules, called spectroscopy.
Contents
History of Molecular Symmetry
Scientists have been thinking about symmetry for a long time! In 1929, a physicist named Hans Bethe used ideas about symmetry to study how ligands (atoms or groups of atoms) connect to a central atom. Later, Eugene Wigner used group theory to explain rules for how atoms give off light.
The first tables that helped organize these symmetry ideas were put together by László Tisza in 1933. Then, Robert Mulliken was the first to publish these tables in English in the same year. These tables helped scientists like E. Bright Wilson predict how molecules would vibrate.
Understanding Symmetry in Molecules
To study how symmetrical a molecule is, chemists use ideas from group theory, which is a part of mathematics.
Symmetry Elements: What Makes a Molecule Symmetrical?
A molecule's symmetry can be described using 5 main types of "symmetry elements." Think of these as imaginary lines, planes, or points that show where a molecule is balanced.
- Symmetry axis (Cn): Imagine a line going through the molecule. If you spin the molecule around this line by a certain angle (like 180 degrees or 120 degrees), and it looks exactly the same as it did before, that line is a symmetry axis. The 'n' tells you how many times it looks the same in a full 360-degree spin. For example, a water molecule has a C2 axis, meaning it looks the same if you spin it 180 degrees. The axis with the highest 'n' is called the principal axis.
- Plane of symmetry (σ): This is like an imaginary mirror cutting through the molecule. If one half of the molecule is a perfect reflection of the other half across this plane, it's a plane of symmetry. Water has two such planes. If the plane is parallel to the principal axis, it's called vertical (σv). If it's perpendicular (at right angles) to the principal axis, it's horizontal (σh).
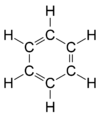
- Center of symmetry (i): This is an imaginary point in the middle of the molecule. If you can draw a straight line from any atom through this center point and find an identical atom an equal distance on the other side, then the molecule has a center of symmetry. The benzene molecule is a good example.
- Rotation-reflection axis (Sn): This is a bit trickier! It's an axis where you first spin the molecule by a certain angle (like a Cn axis), and then you reflect it through a plane that is perpendicular to that axis. If the molecule looks the same after both steps, it has an Sn axis.
- Identity (E): This simply means "no change." Every molecule has this symmetry element because if you do nothing to a molecule, it still looks the same! This element is important for using mathematical group theory.
Symmetry Operations: What You Do to a Molecule
Each symmetry element has one or more "symmetry operations" linked to it. An operation is the actual action you perform, like rotating or reflecting. For example, Ĉn means rotating a molecule around an axis.
Point Groups: Classifying Molecules by Symmetry
A point group is a collection of all the symmetry operations that a molecule has. For a point group, at least one point in the molecule stays in the same place during all these operations.
Scientists use a system called Schoenflies notation to classify molecules into different point groups. There are many different point groups, and each one describes a unique set of symmetries.
What is a Group in Math?
In mathematics, a "group" is a set of things (in our case, symmetry operations) that follow specific rules:
- If you do two operations one after the other, the result must also be an operation in the same group.
- The order in which you combine operations doesn't matter if you're doing three or more (like A(BC) = (AB)C).
- Every group must include the identity operation (E), which means doing nothing.
- For every operation, there must be an "opposite" operation that undoes it, bringing the molecule back to its original state.
The order of a group is simply the total number of symmetry operations in that group.
For example, the water molecule belongs to the C2v point group. Its symmetry operations are E (identity), C2 (180-degree rotation), σv (reflection in one plane), and σv' (reflection in another plane). So, its order is 4.
Another example is the ammonia molecule. It has a C3 rotation axis (it looks the same after spinning 120 degrees) and three mirror planes. Ammonia belongs to the C3v point group, which has an order of 6.
Common Point Groups and Examples
Here's a table showing some common point groups and examples of molecules that belong to them. The "Simple description of typical geometry" column helps you imagine the shape of these molecules.
| Point group | Symmetry operations | Simple description of typical geometry | Example 1 | Example 2 | Example 3 | |
| C1 | E | no symmetry, chiral | 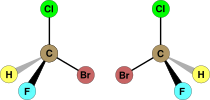 bromochlorofluoromethane (both enantiomers shown) |
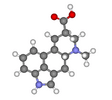 lysergic acid |
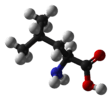 L-leucine and most other α-amino acids except glycine |
|
| Cs | E σh | mirror plane, no other symmetry | 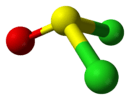 thionyl chloride |
 hypochlorous acid |
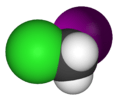 chloroiodomethane |
|
| Ci | E i | inversion center | 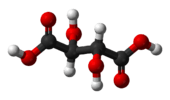 meso-tartaric acid |
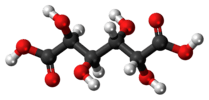 mucic acid (meso-galactaric acid) |
(S,R) 1,2-dibromo-1,2-dichloroethane (anti conformer) | |
| C∞v | E 2C∞ ∞σv | linear |  hydrogen fluoride (and all other heteronuclear diatomic molecules) |
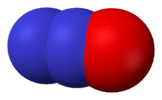 nitrous oxide (dinitrogen monoxide) |
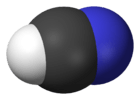 hydrocyanic acid (hydrogen cyanide) |
|
| D∞h | E 2C∞ ∞σi i 2S∞ ∞C2 | linear with inversion center |  oxygen (and all other homonuclear diatomic molecules) |
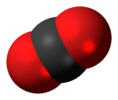 carbon dioxide |
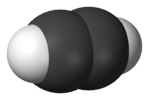 acetylene (ethyne) |
|
| C2 | E C2 | "open book geometry," chiral | 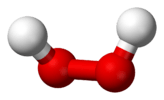 hydrogen peroxide |
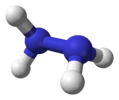 hydrazine |
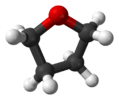 tetrahydrofuran (twist conformation) |
|
| C3 | E C3 | propeller, chiral |  triphenylphosphine |
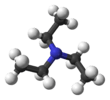 triethylamine |
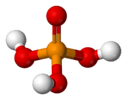 phosphoric acid |
|
| C2h | E C2 i σh | planar with inversion center | 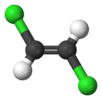 trans-1,2-dichloroethylene |
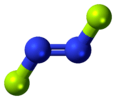 trans-dinitrogen difluoride |
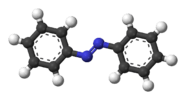 trans-azobenzene |
|
| C3h | E C3 C32 σh S3 S35 | propeller | 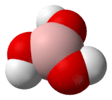 boric acid |
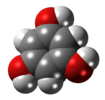 phloroglucinol (1,3,5-trihydroxybenzene) |
||
| C2v | E C2 σv(xz) σv'(yz) | angular (H2O) or see-saw (SF4) |  water |
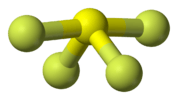 sulfur tetrafluoride |
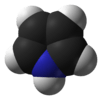 pyrrole |
|
| C3v | E 2C3 3σv | trigonal pyramidal or tetrahedral | 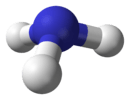 ammonia |
 phosphorus oxychloride |
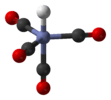 cobalt tetracarbonyl hydride, HCo(CO)4 |
|
| C4v | E 2C4 C2 2σv 2σd | square pyramidal | 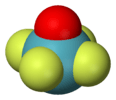 xenon oxytetrafluoride |
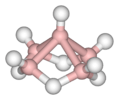 pentaborane(9), B5H9 |
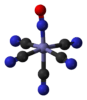 nitroprusside anion [Fe(CN)5(NO)]2− |
|
| C5v | E 2C5 2C52 5σv | 'milking stool' complex | 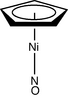 Ni(C5H5)(NO) |
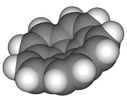 corannulene |
||
| D2 | E C2(x) C2(y) C2(z) | twist, chiral | 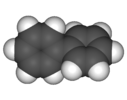 biphenyl (skew conformation) |
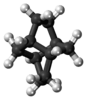 twistane (C10H16) |
cyclohexane twist conformation | |
| D3 | E C3(z) 3C2 | triple helix, chiral | 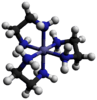 Tris(ethylenediamine)cobalt(III) cation |
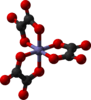 tris(oxalato)iron(III) anion |
||
| D2h | E C2(z) C2(y) C2(x) i σ(xy) σ(xz) σ(yz) | planar with inversion center | 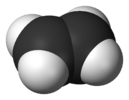 ethylene |
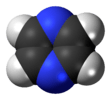 pyrazine |
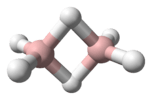 diborane |
|
| D3h | E C3 3C2 σh 2S3 3σv | trigonal planar or trigonal bipyramidal | 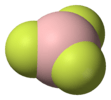 boron trifluoride |
 phosphorus pentachloride |
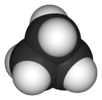 cyclopropane |
|
| D4h | E 2C4 C2 2C2' 2C2 i 2S4 σh 2σv 2σd | square planar | 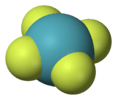 xenon tetrafluoride |
 octachlorodimolybdate(II) anion |
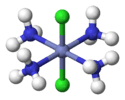 Trans-[CoIII(NH3)4Cl2]+ (excluding H atoms) |
|
| D5h | E 2C5 2C52 5C2 σh 2S5 2S53 5σv | pentagonal |  cyclopentadienyl anion |
 ruthenocene |
 C70 |
|
| D6h | E 2C6 2C3 C2 3C2' 3C2‘’ i 2S3 2S6 σh 3σd 3σv | hexagonal |  benzene |
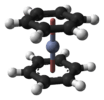 bis(benzene)chromium |
 coronene (C24H12) |
|
| D7h | E C7 S7 7C2 σh 7σv | heptagonal |  tropylium (C7H7+) cation |
|||
| D8h | E C8 C4 C2 S8 i 8C2 σh 4σv 4σd | octagonal |  cyclooctatetraenide (C8H82−) anion |
 uranocene |
||
| D2d | E 2S4 C2 2C2' 2σd | 90° twist |  allene |
 tetrasulfur tetranitride |
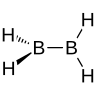 diborane(4) (excited state) |
|
| D3d | E 2C3 3C2 i 2S6 3σd | 60° twist | 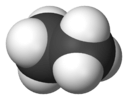 ethane (staggered rotamer) |
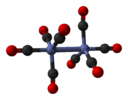 dicobalt octacarbonyl (non-bridged isomer) |
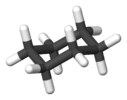 cyclohexane chair conformation |
|
| D4d | E 2S8 2C4 2S83 C2 4C2' 4σd | 45° twist | 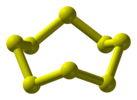 sulfur (crown conformation of S8) |
 dimanganese decacarbonyl (staggered rotamer) |
 octafluoroxenate ion (idealised geometry) |
|
| D5d | E 2C5 2C52 5C2 i 3S103 2S10 5σd | 36° twist |  ferrocene (staggered rotamer) |
|||
| S4 | E 2S4 C2 | 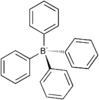 tetraphenylborate anion |
||||
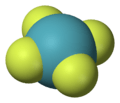
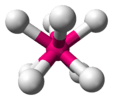
| Td | E 8C3 3C2 6S4 6σd | tetrahedral | 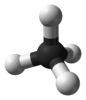 methane |
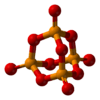 phosphorus pentoxide |
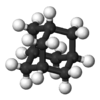 adamantane |
|
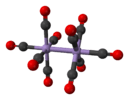
| Oh | E 8C3 6C2 6C4 3C2 i 6S4 8S6 3σh 6σd | octahedral or cubic |  sulfur hexafluoride |
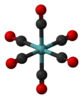 molybdenum hexacarbonyl |
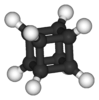 cubane |
|
| Ih | E 12C5 12C52 20C3 15C2 i 12S10 12S103 20S6 15σ | icosahedral or dodecahedral |  Buckminsterfullerene |
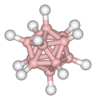 dodecaborate anion |
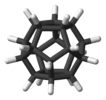 dodecahedrane |
Character Tables: A Symmetry Summary
For each point group, a character table is used to summarize important information about its symmetry operations. These tables also describe how different parts of a molecule (like its orbitals) behave when symmetry operations are applied.
The table is made of "characters," which are numbers (usually 1 or -1).
- A character of 1 means that a part of the molecule (like an orbital) stays the same when a symmetry operation is applied.
- A character of -1 means that it changes sign or direction.
The rows in the table are labeled with letters like A, B, E, and T. These letters tell us about how the molecule's parts behave under rotation:
- A means it's symmetrical when rotated around the main axis.
- B means it's asymmetrical when rotated around the main axis.
- E and T are for more complex situations where multiple parts behave the same way.
If a point group has a center of symmetry, you'll see subscripts like 'g' (for gerade, meaning even, no sign change) or 'u' (for ungerade, meaning uneven, a sign change).
The character table for the C2v symmetry point group (like the water molecule) looks like this:
| C2v | E | C2 | σv(xz) | σv'(yz) | ||
|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | z | x2, y2, z2 |
| A2 | 1 | 1 | -1 | -1 | Rz | xy |
| B1 | 1 | -1 | 1 | -1 | x, Ry | xz |
| B2 | 1 | -1 | -1 | 1 | y, Rx | yz |
For example, in a water molecule (which has C2v symmetry), the 2px orbital of the oxygen atom changes sign with a C2 rotation and a σv'(yz) reflection, but stays the same with the other operations. So, its character set is {1, -1, 1, -1}, which matches the B1 row in the table. This helps chemists understand how electrons are arranged and how molecules react.
Images for kids
See also
 In Spanish: Simetría molecular para niños
In Spanish: Simetría molecular para niños