Euler's totient function Facts for Kids

This graph shows the first thousand values of the Euler totient function.

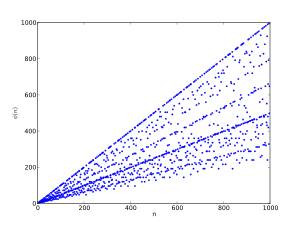
In the world of number theory (which is the study of numbers), the totient of a positive integer (a whole number bigger than zero) n is a special count. It tells you how many positive whole numbers smaller than n do not share any factors with n except for the number 1. When two numbers only share 1 as a factor, they are called coprime.

This special count is often written as 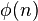$\phi (n)$ . For example, let's look at the number 8. The numbers smaller than 8 are 1, 2, 3, 4, 5, 6, 7.

1 shares no factors with 8 (except 1).
2 shares 2 as a factor with 8.
3 shares no factors with 8 (except 1).
4 shares 2 and 4 as factors with 8.
5 shares no factors with 8 (except 1).
6 shares 2 as a factor with 8.
7 shares no factors with 8 (except 1).

So, the numbers that are coprime to 8 are 1, 3, 5, and 7. There are four of them! This means 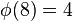$\phi(8) = 4$ .

The function $\phi$ is called the totient function. It's also known as the Euler totient or Euler's totient because a famous Swiss mathematician named Leonhard Euler studied it a lot. People also call it Euler's phi function or just the phi function because the Greek letter Phi (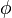 $\phi$ ) is always used for it.

Why is the Euler Totient Function Important?

The totient function is very useful in modular arithmetic, which is like clock arithmetic where numbers "wrap around" after reaching a certain value. It helps us understand how many numbers are "friendly" with a given number in this special kind of math.

One of the most common and important uses of the totient function is in the RSA algorithm. This algorithm is a very popular method of encryption (keeping secret messages safe) that is used all over the world, especially for secure online communication. The Euler totient function is a key part of how RSA works to make sure messages can be sent securely.

For any prime number p (a number that can only be divided by 1 and itself, like 2, 3, 5, 7, etc.), the totient function is very simple: 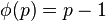$\phi(p) = p-1$ . This is because a prime number doesn't share any factors with the numbers smaller than it, except for 1. So, all the numbers from 1 up to p-1 are coprime to p.

Euler's totient theorem

Euler's totient function facts for kids

Why is the Euler Totient Function Important?

Related pages

See also