Fields Medal facts for kids

Quick facts for kids Fields Medal
The obverse of the Fields Medal
Presented by	International Mathematical Union
Reward	CA$15,000
First awarded	1936; 89 years ago (1936)
Last awarded	2022 (2022)

The Fields Medal is a very important award given to talented mathematicians. It is often called the "Nobel Prize of Mathematics." This special medal is given out every four years. It goes to two, three, or four mathematicians who are under 40 years old. The award is presented at a big meeting called the International Congress of Mathematicians, organized by the International Mathematical Union (IMU). The medal is named after a Canadian mathematician named John Charles Fields.

Many people consider the Fields Medal one of the highest honors a mathematician can get. It is seen as the top award in mathematics around the world. Since 2006, the winners also receive a money prize of CA$15,000. John Charles Fields helped create this award and even designed the medal himself. He also helped fund the money part of the prize.

The first Fields Medals were given out in 1936. The winners were Lars Ahlfors from Finland and Jesse Douglas from the United States. Since 1950, the medal has been awarded every four years. Its main goal is to recognize and support young mathematicians who have done amazing work. In 2014, Maryam Mirzakhani from Iran became the first woman to win the Fields Medal. As of 2022, 64 people have received this award.

The most recent Fields Medal winners received their awards on July 5, 2022. This event was held online and streamed live from Helsinki, Finland. It was originally planned for Saint Petersburg, Russia, but was moved.

What Makes Someone a Fields Medal Winner?

The Fields Medal is known as the most important award in mathematics. It is different from the Nobel Prize in a few ways.

Age Limit for the Award

One big difference is that the Fields Medal has an age limit. A mathematician must be under 40 years old on January 1 of the year they receive the medal. This rule was put in place because John Charles Fields wanted the award to encourage young mathematicians to keep doing great work. He also hoped it would inspire others.

How Often is the Medal Given?

Unlike the Nobel Prize, which is given every year, the Fields Medal is only awarded every four years. Also, a person can only win the Fields Medal once. If you win it, you cannot win it again in the future.

Who Has Won the Fields Medal?

The medal was first given in 1936. By 2022, 64 people had won it. Most winners have a PhD in mathematics. However, two winners, Edward Witten and Martin Hairer, had PhDs in physics.

Famous Fields Medal Winners

Sometimes, the Fields Medal winners are recognized for specific mathematical achievements. Other times, the reasons are more general. However, for every winner, other famous mathematicians give talks about their work at the International Congress of Mathematicians. The next Fields Medal awards are planned for 2026 in Philadelphia.

Year	Meeting Location	Winners		University or Institute (when awarded)	University or Institute (current or last)	Why They Won
1936	Oslo, Norway		Ahlfors, LarsLars Ahlfors	University of Helsinki, Finland	Harvard University, US	"For his research on surfaces and functions. He opened up new areas in mathematics."
			Douglas, JesseJesse Douglas	Massachusetts Institute of Technology, US	City College of New York, US	"For important work on the Plateau problem, which is about finding the smallest surfaces connecting fixed boundaries."
1950	Cambridge, US		Schwartz, LaurentLaurent Schwartz	University of Nancy, France	University of Paris VII, France	"He created the theory of distributions, a new way to understand generalized functions."
			Selberg, AtleAtle Selberg	Institute for Advanced Study, US	Institute for Advanced Study, US	"He improved methods for finding prime numbers and made big discoveries about the Riemann zeta function."
1954	Amsterdam, Netherlands		Kodaira, KunihikoKunihiko Kodaira	Princeton University, US, University of Tokyo, Japan and Institute for Advanced Study, US	University of Tokyo, Japan	"For major discoveries in the theory of harmonic integrals and their uses in algebraic varieties."
			Serre, Jean-PierreJean-Pierre Serre	University of Nancy, France	Collège de France, France	"He made big discoveries about the homotopy groups of spheres and used sheaves to improve complex variable theory."
1958	Edinburgh, UK		Roth, KlausKlaus Roth	University College London, UK	Imperial College London, UK	"For solving a famous problem in number theory related to the Thue-Siegel inequality."
			Thom, RenéRené Thom	University of Strasbourg, France	Institut des Hautes Études Scientifiques, France	"For creating the theory of 'Cobordisme,' which helped understand the shape of differentiable manifolds."
1962	Stockholm, Sweden		Hörmander, LarsLars Hörmander	Stockholm University, Sweden	Lund University, Sweden	"He worked on partial differential equations, especially the theory of linear differential operators."
			Milnor, JohnJohn Milnor	Princeton University, US	Stony Brook University, US	"He showed that a 7-dimensional sphere can have different structures, leading to the field of differential topology."
1966	Moscow, USSR		Atiyah, MichaelMichael Atiyah	University of Oxford, UK	University of Edinburgh, UK	"For his work with Hirzebruch on K-theory and his proof of the Atiyah–Singer index theorem."
			Cohen, PaulPaul Cohen	Stanford University, US	Stanford University, US	"He used a method called 'forcing' to prove that certain ideas in set theory are independent."
			Grothendieck, AlexanderAlexander Grothendieck	Institut des Hautes Études Scientifiques, France	Centre National de la Recherche Scientifique, France	"He made huge progress in algebraic geometry and introduced the idea of K-theory."
			Smale, StephenStephen Smale	University of California, Berkeley, US	City University of Hong Kong, Hong Kong	"He worked in differential topology and proved the generalized Poincaré conjecture for certain dimensions."
1970	Nice, France		Baker, AlanAlan Baker	University of Cambridge, UK	Trinity College, Cambridge, UK	"He generalized a theorem about numbers and found new types of transcendental numbers."
			Hironaka, HeisukeHeisuke Hironaka	Harvard University, US	Kyoto University, Japan	"He extended work on the resolution of singularities on an algebraic variety to any dimension."
			Novikov, SergeiSergei Novikov	Moscow State University, USSR	Steklov Mathematical Institute, Russia Moscow State University, Russia University of Maryland-College Park, US	"He made important advances in topology, including proving the topological invariance of Pontryagin classes."
			Thompson, John G.John G. Thompson	University of Cambridge, UK	University of Cambridge, UK University of Florida, US	"He proved that all non-cyclic finite simple groups have an even order, working with W. Feit."
1974	Vancouver, Canada		Bombieri, EnricoEnrico Bombieri	University of Pisa, Italy	Institute for Advanced Study, US	"He made major contributions to prime numbers, functions, and partial differential equations."
			Mumford, DavidDavid Mumford	Harvard University, US	Brown University, US	"He helped solve problems about the existence and structure of varieties of moduli and contributed to algebraic surfaces."
1978	Helsinki, Finland		Deligne, PierrePierre Deligne	Institut des Hautes Études Scientifiques, France	Institute for Advanced Study, US	"He solved the three Weil conjectures, which helped connect algebraic geometry and number theory."
			Fefferman, CharlesCharles Fefferman	Princeton University, US	Princeton University, US	"He brought new ideas to the study of complex analysis in multiple dimensions."
			Margulis, GrigoryGrigory Margulis	Moscow State University, USSR	Yale University, US	"He provided new ways to analyze the structure of Lie groups, connecting different math fields."
			Quillen, DanielDaniel Quillen	Massachusetts Institute of Technology, US	University of Oxford, UK	"He was the main creator of higher algebraic K-theory, a new tool for solving problems in algebra."
1982	Warsaw, Poland		Connes, AlainAlain Connes	Institut des Hautes Études Scientifiques, France	Institut des Hautes Études Scientifiques, France Collège de France, France Ohio State University, US	"He contributed to the theory of operator algebras and their uses in geometry."
			Thurston, WilliamWilliam Thurston	Princeton University, US	Cornell University, US	"He changed how we study topology in 2 and 3 dimensions, showing links between analysis, topology, and geometry."
			Yau, Shing-TungShing-Tung Yau	Institute for Advanced Study, US	Tsinghua University, China	"He made contributions to differential equations, the Calabi conjecture, and general relativity theory."
1986	Berkeley, US		Donaldson, SimonSimon Donaldson	University of Oxford, UK	Imperial College London, UK Stony Brook University, US	"For his work on the topology of four-manifolds, showing that Euclidean four-space can have a different structure."
			Faltings, GerdGerd Faltings	Princeton University, US	Max Planck Institute for Mathematics, Germany	"For proving the Mordell Conjecture using methods from arithmetic algebraic geometry."
			Freedman, MichaelMichael Freedman	University of California, San Diego, US	Microsoft Station Q, US	"He developed new ways to analyze the topology of four-manifolds, including proving the Generalized Poincaré conjecture in four dimensions."
1990	Kyoto, Japan		Drinfeld, VladimirVladimir Drinfeld	B Verkin Institute for Low Temperature Physics and Engineering, USSR	University of Chicago, US	"His work on Langlands' program and quantum groups was a major breakthrough."
			Jones, VaughanVaughan Jones	University of California, Berkeley, US	University of California, Berkeley, US Vanderbilt University, US	"He found an amazing connection between von Neumann algebras and geometric topology, leading to a new way to describe knots."
			Mori, ShigefumiShigefumi Mori	Kyoto University, Japan	Kyoto University, Japan	"He made huge advances in algebraic geometry with his 'Mori's Program' for classifying algebraic varieties."
			Witten, EdwardEdward Witten	Institute for Advanced Study, US	Institute for Advanced Study, US	"He surprised mathematicians with brilliant uses of physics ideas to prove new and deep mathematical theorems."
1994	Zürich, Switzerland		Bourgain, JeanJean Bourgain	Institut des Hautes Études Scientifiques, France	Institute for Advanced Study, US	"His work touched on many central areas of mathematical analysis, including the geometry of Banach spaces and partial differential equations."
			Lions, Pierre-LouisPierre-Louis Lions	University of Paris 9, France	Collège de France, France École polytechnique, France	"His contributions cover many areas, from probability theory to partial differential equations, often motivated by real-world uses."
			Yoccoz, Jean-ChristopheJean-Christophe Yoccoz	Paris-Sud 11 University, France	Collège de France, France	"He provided a clear proof of Bruno's theorem and its opposite, and worked on systems of conjugation invariants."
			Zelmanov, EfimEfim Zelmanov	University of Wisconsin-Madison University of Chicago, US	Steklov Mathematical Institute, Russia, University of California, San Diego, US	"For solving the restricted Burnside problem."
1998	Berlin, Germany		Borcherds, RichardRichard Borcherds	University of California, Berkeley, US University of Cambridge, UK	University of California, Berkeley, US	"For his work in algebra, automorphic forms, and mathematical physics, including proving the Conway–Norton moonshine conjecture."
			Gowers, TimothyTimothy Gowers	University of Cambridge, UK	University of Cambridge, UK	"For his work in functional analysis and combinatorics, developing new ideas about infinite-dimensional geometry."
			Kontsevich, MaximMaxim Kontsevich	Institut des Hautes Études Scientifiques, France Rutgers University, US	Institut des Hautes Études Scientifiques, France Rutgers University, US	"For his work in algebraic geometry, topology, and mathematical physics, including proving Witten's conjecture."
			McMullen, Curtis T.Curtis T. McMullen	Harvard University, US	Harvard University, US	"For his work in holomorphic dynamics and the geometry of three-manifolds, including proving Bers' conjecture."
2002	Beijing, China		Lafforgue, LaurentLaurent Lafforgue	Institut des Hautes Études Scientifiques, France	Institut des Hautes Études Scientifiques, France	"For proving the Langlands correspondence for linear groups over function fields."
			Voevodsky, VladimirVladimir Voevodsky	Institute for Advanced Study, US	Institute for Advanced Study, US	"He created and developed motivic cohomology and A1-homotopy theory, and proved the Milnor conjectures."
2006	Madrid, Spain		Okounkov, AndreiAndrei Okounkov	Princeton University, US	Columbia University, US University of California, Berkeley, US	"For his work connecting probability, representation theory, and algebraic geometry."
			Perelman, GrigoriGrigori Perelman (declined)	None	St. Petersburg Department of Steklov Institute of Mathematics of Russian Academy of Sciences, Russia	"For his work in geometry and new ideas about the Ricci flow."
			Tao, TerenceTerence Tao	University of California, Los Angeles, US	University of California, Los Angeles, US	"For his work in partial differential equations, combinatorics, harmonic analysis, and number theory."
			Werner, WendelinWendelin Werner	Paris-Sud 11 University, France	ETH Zurich, Switzerland	"For his work on stochastic Loewner evolution, the geometry of two-dimensional Brownian motion, and conformal field theory."
2010	Hyderabad, India		Lindenstrauss, ElonElon Lindenstrauss	Hebrew University of Jerusalem, Israel Princeton University, US	Hebrew University of Jerusalem, Israel	"For his results on measure rigidity in ergodic theory and their uses in number theory."
			Ngô Bảo Châu	Paris-Sud 11 University, France Institute for Advanced Study, US	University of Chicago, US Institute for Advanced Study, US	"For proving the Fundamental Lemma in the theory of automorphic forms using new geometric methods."
			Smirnov, StanislavStanislav Smirnov	University of Geneva, Switzerland	University of Geneva, Switzerland St. Petersburg State University, Russia	"For proving the conformal invariance of percolation and the planar Ising model in physics."
			Villani, CédricCédric Villani	École Normale Supérieure de Lyon, France Institut Henri Poincaré, France	Lyon University, France Institut Henri Poincaré, France	"For his proofs of nonlinear Landau damping and how systems reach equilibrium for the Boltzmann equation."
2014	Seoul, South Korea		Avila, ArturArtur Avila	University of Paris VII, France CNRS, France Instituto Nacional de Matemática Pura e Aplicada, Brazil	University of Zurich, Switzerland Instituto Nacional de Matemática Pura e Aplicada, Brazil	"For his deep contributions to dynamical systems theory, using the idea of renormalization."
			Bhargava, ManjulManjul Bhargava	Princeton University, US	Princeton University, US	"For creating powerful new methods in the geometry of numbers, used to count rings and understand elliptic curves."
			Hairer, MartinMartin Hairer	University of Warwick, UK	École Polytechnique Fédérale de Lausanne, Switzerland Imperial College London, UK	"For his great contributions to the theory of stochastic partial differential equations, especially creating a theory of regularity structures."
			Mirzakhani, MaryamMaryam Mirzakhani	Stanford University, US	Stanford University, US	"For her outstanding contributions to the dynamics and geometry of Riemann surfaces and their moduli spaces."
2018	Rio de Janeiro, Brazil		Birkar, CaucherCaucher Birkar	University of Cambridge, UK	University of Cambridge, UK	"For proving the boundedness of Fano varieties and his work on the minimal model program."
			Figalli, AlessioAlessio Figalli	Swiss Federal Institute of Technology Zurich, Switzerland	Swiss Federal Institute of Technology Zurich, Switzerland	"For his contributions to the theory of optimal transport and its uses in partial differential equations, metric geometry, and probability."
			Scholze, PeterPeter Scholze	University of Bonn, Germany	University of Bonn, Germany	"For changing arithmetic algebraic geometry over p-adic fields."
			Venkatesh, AkshayAkshay Venkatesh	Stanford University, US	Institute for Advanced Study, US	"For combining analytic number theory, homogeneous dynamics, topology, and representation theory to solve long-standing problems."
2022	Helsinki, Finland		Duminil-Copin, HugoHugo Duminil-Copin	Institut des Hautes Études Scientifiques, France University of Geneva, Switzerland	Institut des Hautes Études Scientifiques, France University of Geneva, Switzerland	"For solving long-standing problems in the probabilistic theory of phase transitions in statistical physics."
			Huh, JuneJune Huh	Princeton University, US	Princeton University, US	"For bringing ideas from Hodge theory to combinatorics and proving several important conjectures."
			Maynard, JamesJames Maynard	University of Oxford, UK	University of Oxford, UK	"For his contributions to analytic number theory, which have greatly improved our understanding of prime numbers."
			Viazovska, MarynaMaryna Viazovska	École Polytechnique Fédérale de Lausanne, Switzerland	École Polytechnique Fédérale de Lausanne, Switzerland	"For proving that the 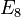lattice provides the densest packing of identical spheres in 8 dimensions."

Key Moments in Fields Medal History

The Fields Medal has a rich history with many interesting moments.

First Winners and Youngest Recipient

The medal was first given in 1936 to Lars Ahlfors and Jesse Douglas. Its goal is to encourage young mathematicians. In 1954, Jean-Pierre Serre became the youngest person to win the Fields Medal at just 27 years old. He still holds this record.

Notable Absences and Protests

• In 1966, Alexander Grothendieck chose not to attend the meeting in Moscow. He was protesting against Soviet military actions. Another person accepted the medal for him.
• In 1970, Sergei Novikov could not travel to the meeting in Nice to get his medal because of rules set by the Soviet government.
• In 1978, Grigory Margulis also could not travel to Helsinki to receive his medal due to Soviet government rules. Someone else accepted it for him.

Changes and Special Recognitions

• In 1982, the meeting was supposed to be in Warsaw, Poland. However, it had to be moved to the next year because of martial law in Poland. The awards were still announced earlier that year.
• In 1990, Edward Witten became the first physicist to win the award.
• In 1998, Andrew Wiles received a special silver plaque from the IMU. This was to honor his proof of Fermat's Last Theorem. He was too old for the Fields Medal at that time, but his work was incredibly important.
• In 2006, Grigori Perelman, who proved the famous Poincaré conjecture, refused his Fields Medal. He did not attend the meeting.
• In 2014, Maryam Mirzakhani became the first woman and first Iranian to win the Fields Medal. Artur Avila became the first South American winner, and Manjul Bhargava was the first person of Indian origin to win.
• In 2022, Maryna Viazovska became the first Ukrainian to win the Fields Medal. June Huh became the first person of Korean ancestry to receive the award.

About the Medal Itself

The reverse of the Fields Medal

The Fields Medal was designed by a Canadian sculptor named R. Tait McKenzie. It is made of 14-karat gold. It is about 63.5 millimeters wide and weighs 169 grams.

What's on the Front?

On the front side of the medal, you can see a picture of Archimedes, a famous ancient Greek mathematician. There is also a quote in Latin that means: "To surpass one's understanding and master the world." The year 1933 is written in Roman numerals, but it has a small mistake. The word "of Archimedes" is also written in Greek letters.

What's on the Back?

The back of the medal has a Latin inscription that translates to: "Mathematicians gathered from the entire world have awarded [this prize] for outstanding writings." In the background, you can see a picture of Archimedes' tomb. It shows a carving that illustrates his famous theorem about the sphere and cylinder. This theorem was about the relationship between the volumes of a sphere and a cylinder around it. Archimedes was very proud of this discovery.

The name of the winner is engraved around the edge of the medal.

Women Who Have Won the Fields Medal

So far, two women have received the Fields Medal:

• Maryam Mirzakhani from Iran in 2014
• Maryna Viazovska from Ukraine in 2022

Related Awards

See also

In Spanish: Medalla Fields para niños