Grégoire de Saint-Vincent facts for kids
.jpg)
Grégoire de Saint-Vincent (born September 8, 1584, in Bruges – died June 5, 1667, in Ghent) was a Flemish Jesuit priest and a brilliant mathematician. He is best known for his important work on finding the area under a special curve called a hyperbola. This work helped lead to the idea of logarithms.
Grégoire also gave a very clear explanation of how to add up a geometric series. This is a list of numbers where each number is found by multiplying the previous one by a fixed number. He even used this idea to solve Zeno's paradox, which is a famous puzzle about motion. He showed that even if time intervals get smaller and smaller, they can still add up to a specific, finite amount of time.
Contents
Life of Grégoire de Saint-Vincent
Grégoire was born in Bruges on September 8, 1584. After studying philosophy, he joined the Society of Jesus (the Jesuits) in 1605. His amazing talent for mathematics was recognized by a famous mathematician named Christopher Clavius in Rome.
Grégoire was sent to Louvain in 1612 and became a priest in 1613. From 1617 to 1620, he taught mathematics in Antwerp with François d'Aguilon. He then moved to Louvain in 1621 and taught math there until 1625. Around this time, he became very focused on a famous math problem called "squaring the circle". This problem involves trying to draw a square with the exact same area as a given circle, using only a compass and a straightedge. He wanted to publish his method, but his superiors asked another mathematician, Christoph Grienberger, to review it first.
In 1625, Grégoire traveled to Rome to talk with Grienberger, but he wasn't successful. He returned to the Netherlands in 1627. The next year, he went to Prague to work for Emperor Ferdinand II. After he became ill, another mathematician, Theodorus Moretus, helped him. In 1631, when the Saxons attacked Prague, Grégoire had to leave, and some of his important writings were lost. Luckily, some of them were returned to him in 1641.
From 1632, Grégoire lived with the Jesuit community in Ghent and continued to teach mathematics. During his time in Antwerp, his mathematical ideas really grew. He started using infinite series, the special properties of the hyperbola, and a method called "exhaustion" to solve problems. He later used these ideas in his theory called ductus plani in planum.
Ductus Plani in Planum
One of Grégoire de Saint-Vincent's big contributions was in his book Opus Geometricum. In this book, he used a method he called ductus plani in planum. This method was a clever way to figure out the volumes of many different 3D shapes.
Imagine you have a flat shape, like a square or a triangle. The ductus plani in planum method was a way to "move" or "stretch" this flat shape to create a 3D solid. It was a very important idea because, at that time, mathematicians didn't have the algebraic notation or integral calculus that we use today to find volumes. So, Grégoire's geometric way of transforming shapes was very useful.
For example, he described shapes like the "ungula." An ungula is created when you cut a cylinder (like a can) with a slanted flat surface that goes through the bottom edge. He also described a "double ungula" made from two cylinders crossing each other. Later, another famous mathematician, Blaise Pascal, used these ideas in his own work.
Grégoire wrote his manuscript for Opus Geometricum in the 1620s, but it wasn't published until 1647. When it finally came out, it got a lot of attention. This was because of his systematic way of finding volumes, which he called ductus plani in planum. This method, which means "drawing a plane into a plane," is explained in Book VII of his Opus Geometricum.
When it came to finding the area under a hyperbola, Grégoire was very close to discovering the link between this area and logarithms. He did everything except clearly state that connection.
Quadrature of the Hyperbola
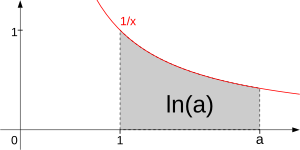
Grégoire de Saint-Vincent made a very important discovery about the area under a special curve called a rectangular hyperbola. This curve is described by the equation xy = k (where k is a constant number). He found that the area under this curve between two points, say a and b, is the same as the area between two other points, c and d, if the ratio of the points is the same. This means if a divided by b is equal to c divided by d.
This discovery was a big step towards understanding hyperbolic logarithms. It allowed mathematicians to define a function, let's call it A(x), which represents the area under the curve from 1 to x. This function has a special property: A(xy) = A(x) + A(y). This property is exactly what defines a logarithm! When you multiply numbers, their logarithms add up. If you choose the specific hyperbola xy = 1, you get what we now call the natural logarithm.
A student and colleague of Saint-Vincent, A. A. de Sarasa, noticed that this area property of the hyperbola was indeed a type of logarithm. It was a way to turn multiplication problems into simpler addition problems.
In 1651, Christiaan Huygens, another famous scientist, published his work on finding the area of hyperbolas, ellipses, and circles. He mentioned Saint-Vincent's work in his writings.
The problem of finding the area of the hyperbola was also studied by James Gregory in 1668. While Gregory knew about Saint-Vincent's work, he developed his own method using shapes drawn inside and outside the curve. In the same year, Nicholas Mercator introduced the term natural logarithm.
In 1688, Grégoire de Saint-Vincent was praised as "Magnan" and "Learned." People recognized his great work in showing that distances along the side of a hyperbola, when they follow a geometric pattern, are related to the areas under the curve.
Historians of calculus later noted that by the 1660s, thanks to the work of Gregory St. Vincent and de Sarasa, it was widely known that the area under the hyperbola y = 1/x was connected to the logarithm of the ratio of the y-values at the ends of the segment.
Works
See also
- History of logarithms
Images for kids
-
Grégoire de Saint-Vincent
-
Front page of Saint-Vincent's Opus Geometricum
-
The natural logarithm of a number a can be seen as the area under the curve f(x) = 1/x from 1 to a.
-
Opus geometricum posthumum, published in 1668
