Iwasawa theory facts for kids

Iwasawa theory is a part of number theory, which is the study of numbers. It looks at special groups called ideal class groups. This theory was started by a mathematician named Kenkichi Iwasawa in the 1950s. He developed it while studying cyclotomic fields, which are special number systems.

Later, in the 1970s, Barry Mazur thought about using Iwasawa theory for other mathematical objects called Abelian Varieties. In the 1990s, Ralph Greenberg suggested applying it to motives, which are even more complex mathematical ideas.

How Iwasawa Theory Works

Iwasawa noticed that there are special "towers" of number systems in algebraic number theory. These towers have a special kind of symmetry, described by a group called the Galois group. This group is similar to the additive group of p-adic integers. We usually write this group as Γ (Gamma).

The group Γ is like an infinite collection of groups that get bigger and bigger, connected in a special way. It helps mathematicians understand how these number systems behave.

An Example

Let's look at an example to understand this better. Imagine a special number called 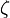, which is a "primitive 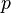-th root of unity." This means that if you multiply 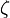by itself 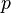times, you get 1.

Iwasawa looked at a tower of number fields like this: 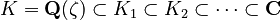Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): K = \mathbf{Q} (\zeta) \subset K_{1} \subset K_{2} \subset \cdots \subset \mathbf{C}

Here, 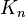is a field made from a "primitive 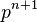-th root of unity." This tower of fields keeps growing. The Galois group of this whole tower over 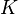is like the Γ group we talked about.

To make things interesting, Iwasawa looked at the "ideal class group" of each 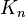. He focused on a specific part of it, called the 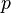-torsion part, which we can call 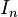. These 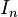groups are connected by "norm mappings." This creates an "inverse limit" group, which we call 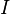. The Γ group acts on 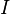, and understanding this action is key to Iwasawa theory.

Why is it Important?

One big reason Iwasawa theory is important goes back to Fermat's Last Theorem. This famous theorem states that no three positive integers 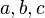can satisfy the equation 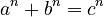Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a^n + b^n = c^n for any integer value of greater than 2.

The mathematician Kummer found that a certain part of the ideal class group (the 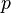-torsion part) was a major challenge in proving Fermat's Last Theorem directly. What Iwasawa did was to extend Kummer's ideas "to infinity" in a new way.

The group 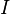is a special kind of mathematical object called a "module" over a "group ring" . This group ring is well-behaved, which means mathematicians can study its modules in a structured way.

History of Iwasawa Theory

Iwasawa theory started in the 1950s and has grown into a large field of study. A key discovery was the link between this module theory and "p-adic L-functions." These functions were defined in the 1960s by Kubota and Leopoldt.

P-adic L-functions are like special versions of other functions called Dirichlet L-functions, but they work with "p-adic numbers." They are defined using Bernoulli numbers and a process called interpolation. This connection showed that Iwasawa theory could help move beyond Kummer's century-old results on regular primes.

The Main Conjecture

A very important idea in Iwasawa theory is the main conjecture of Iwasawa theory. This conjecture says that two different ways of defining p-adic L-functions should match up. One way is through the module theory of Iwasawa, and the other is through interpolation.

This main conjecture was eventually proven by Barry Mazur and Andrew Wiles for a specific number field called Q (the rational numbers). Andrew Wiles later proved it for all "totally real number fields." These proofs were inspired by Ken Ribet's work on the Herbrand-Ribet theorem.

More recently, other mathematicians like Chris Skinner and Eric Urban have announced proofs of a "main conjecture" for other mathematical objects. An easier way to prove the Mazur-Wiles theorem was found using "Euler systems," developed by Kolyvagin. Other generalizations of the main conjecture have also been proven using this method, including by Karl Rubin.

• Greenberg, Ralph, Iwasawa Theory - Past & Present, Advanced Studies in Pure Math. 30 (2001), 335-385. Available at [1].
• Coates, J. and Sujatha, R., Cyclotomic Fields and Zeta Values, Springer-Verlag, 2006
• Lang, S., Cyclotomic Fields, Springer-Verlag, 1978
• Washington, L., Introduction to Cyclotomic Fields, 2nd edition, Springer-Verlag, 1997

See also

In Spanish: Teoría de Iwasawa para niños