Law of excluded middle Facts for Kids

The Law of Excluded Middle is a basic rule in logic. It says that for any statement, it must be either true or false. There is no "middle" option. Think of it like a light switch: it's either ON or OFF. It can't be somewhere in between.

This law is one of the "three laws of thought." The others are the law of noncontradiction (a statement cannot be both true and false at the same time) and the law of identity (a thing is what it is). These laws help us understand how logic works.

The Law of Excluded Middle is also known as the principle of the excluded third. In Latin, it's called principium tertii exclusi, which means "the principle of the excluded third." Another Latin phrase for it is tertium non datur, meaning "no third possibility is given." In classical logic, this law is always true.

It's important not to confuse this law with the idea of principle of bivalence. Bivalence says every statement is either true or false. The Law of Excluded Middle is about a statement and its opposite. If a statement is true, its opposite is false. If the statement is false, its opposite is true.

History of the Law of Excluded Middle
- Aristotle's Ideas
- Bertrand Russell and Principia Mathematica
Examples of the Law of Excluded Middle
- Proving Things with the Law
- Non-Constructive Proofs
Criticisms of the Law
- Paradoxes
See also

History of the Law of Excluded Middle

Aristotle's Ideas

The first known mention of this idea comes from the ancient Greek philosopher Aristotle. He talked about it in his writings, like On Interpretation and Metaphysics.

Aristotle said that for any two statements that contradict each other (like "it is raining" and "it is not raining"), one must be true and the other must be false. He believed there couldn't be anything in between these two options.

He explained that confusion might come from using words that have more than one meaning. But the facts themselves cannot be unclear. For example, "being a man" cannot mean "not being a man" at the same time. A thing cannot both be and not be the same thing.

Aristotle also wrote that "there cannot be an intermediate between contradictories." This means you must either say something is true or say it is not true. There is no middle ground. This is a very clear way of stating the Law of Excluded Middle.

However, Aristotle also discussed future events. He wondered if statements about things that haven't happened yet (like "there will be a sea battle tomorrow") follow this law. He thought they might not.

Bertrand Russell and Principia Mathematica

Later, in the early 1900s, logicians Bertrand Russell and Alfred North Whitehead wrote a very important book called Principia Mathematica. In this book, they formally stated the Law of Excluded Middle as a key rule in logic.

They defined "truth-values" as simply "truth" if a statement is true, and "falsehood" if it is false. They showed how this law helps build other important logical tools.

For example, they showed that if a statement P is true, then it's not true that P is false. This is called the "principle of double negation." It means that saying "it's not true that it's not raining" is the same as saying "it is raining."

Examples of the Law of Excluded Middle

Let's look at some simple examples to understand this law better.

If we have the statement:

Socrates is mortal.

The Law of Excluded Middle says that the following statement must be true:

Either Socrates is mortal, or it is not the case that Socrates is mortal.

There is no other option. Socrates cannot be neither mortal nor not-mortal. So, one of those two possibilities must be true.

Proving Things with the Law

The Law of Excluded Middle is often used in mathematical proofs. Sometimes, it helps prove that something exists without actually showing you how to find it. This is called a non-constructive proof.

Here's an example: We want to prove that there are two irrational numbers (numbers that cannot be written as a simple fraction) a and b, such that a raised to the power of b (written as a^b) is a rational number (a number that can be written as a simple fraction).

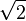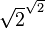We know that the square root of 2 ( $\sqrt{2}$ ) is an irrational number. Let's consider the number $\sqrt{2}^{\sqrt{2}}$ .

Now, here's where the Law of Excluded Middle comes in: This number (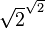 $\sqrt{2}^{\sqrt{2}}$ ) is either rational or irrational. There's no third option.

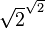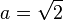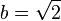Case 1: If $\sqrt{2}^{\sqrt{2}}$ is a rational number, then we're done! We can choose $a=\sqrt{2}$ and $b=\sqrt{2}$ . Both are irrational, and their power is rational.

Case 2: If 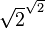$\sqrt{2}^{\sqrt{2}}$ is an irrational number, then let's try something else.

Let 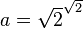Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a = \sqrt{2}^{\sqrt{2}} (which we are assuming is irrational) and 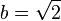Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): b = \sqrt{2} (which we know is irrational). Now, let's calculate 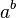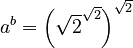$a^b$ : Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a^b = \left(\sqrt{2}^{\sqrt{2}}\right)^{\sqrt{2}} Using rules of exponents, this becomes: 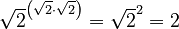Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{2}^{\left(\sqrt{2}\cdot\sqrt{2}\right)} = \sqrt{2}^2 = 2 . Since 2 is a rational number, we have found our a and b!

This proof works because we used the Law of Excluded Middle to say the number had to be one of two things (rational or irrational). We didn't need to know which one it actually was to complete the proof.

Non-Constructive Proofs

Some mathematicians, called intuitionists, don't like these "non-constructive" proofs. They believe that to prove something exists, you should be able to actually "construct" or find it.

For example, in the proof above, we didn't actually figure out if 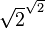$\sqrt{2}^{\sqrt{2}}$ is rational or irrational. We just said it had to be one or the other. Intuitionists would want a way to actually find the specific numbers a and b that work.

Intuitionists also disagree with using the Law of Excluded Middle when dealing with infinite sets (like all numbers). They say we can't check every single number in an infinite set, so we can't say for sure that a property is either true or false for every member of that set. For finite sets (like a group of 10 apples), they agree the law works.

Criticisms of the Law

Some modern logic systems use a different idea called "negation as failure." Instead of a statement being true or false, it's either true or "not able to be proved true." This is used in computer programming logic. In these systems, the Law of Excluded Middle isn't automatically built in, but a programmer can choose to use it.

Mathematicians like L. E. J. Brouwer have also questioned if the Law of Excluded Middle is always useful in modern mathematics.

Paradoxes

Sometimes, statements can cause problems for the Law of Excluded Middle. A famous example is the "Liar's paradox":

This statement is false.

If this statement is true, then it must be false (because it says it's false). But if it's false, then it must be true (because it says it's false, and it is). This seems to be a statement that is neither true nor false, which challenges the Law of Excluded Middle. However, some logicians argue that the negation of this statement ("This statement is not false") can be assigned true, so the law still holds.

Another example is Russell's paradox in set theory. It talks about "the set of all sets that do not contain themselves." Does this set contain itself? If it does, then it shouldn't (because it only contains sets that don't contain themselves). If it doesn't, then it should (because it's a set that doesn't contain itself). This also leads to a contradiction. Modern set theory has ways to avoid this kind of paradox.

Law of excluded middle facts for kids

Contents