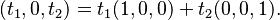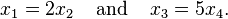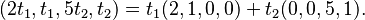Linear subspace facts for kids

Imagine a grid of points, like a checkerboard. Here, we see one-dimensional lines (subspaces) within a two-dimensional space. The green circles show the starting point (0,0), which is part of all these lines. Each of the other 24 points belongs to only one line. This idea works for any number of dimensions!

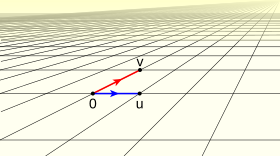
In mathematics, especially in a field called linear algebra, a linear subspace (or just subspace) is like a smaller vector space that lives inside a bigger one. Think of it as a special part of a larger space that still follows all the rules of a vector space itself.

For example, a line that goes through the origin (0,0) in a 2D plane is a subspace. A plane that goes through the origin in a 3D space is also a subspace.

What is a Subspace?

Imagine you have a big vector space called V. A subset W of V is a linear subspace if it meets two important rules:

Rule 1: If you take any two vectors from W and add them together, their sum must also be in W.
Rule 2: If you take any vector from W and multiply it by any number (called a scalar), the result must also be in W.

Also, a subspace must always include the zero vector (the point at the origin, like (0,0) or (0,0,0)). If a set follows these rules, it's a subspace!

Every vector space always has at least two simple subspaces:

The zero vector space, which only contains the zero vector.
The entire vector space itself.

These are often called the trivial subspaces.

Examples of Subspaces

Let's look at some examples to make this clearer.

Example I: Flat Planes in 3D Space

Imagine the 3D space we live in, which mathematicians call R³. This space includes all points like (x, y, z). Now, let's consider a set W of all points in R³ where the last number (z) is always 0. So, points in W look like (x, y, 0). This is like the floor of a room if the origin (0,0,0) is a corner.

Proof that W is a subspace:

Rule 1 (Adding Vectors):

* Take two points from W: {{{1}}} and {{{1}}}. * Add them: {{{1}}}. * Notice the last number is still 0. So, the sum is also in W.

Rule 2 (Multiplying by a Scalar):

* Take a point from W: {{{1}}}. * Take any number c. Multiply: {{{1}}}. * Again, the last number is 0. So, the result is also in W. Since both rules work, W is a subspace!

Example II: Lines in 2D Space

Let's look at the 2D plane, called R². Points here look like (x, y). Consider a set W where the first number (x) is always equal to the second number (y). So, points in W look like (x, x). This forms a straight line that goes through the origin.

Example II Illustrated: The green line shows a subspace where x=y.

Proof that W is a subspace:

Rule 1 (Adding Vectors):

* Take two points from W: {{{1}}} and {{{1}}}. * Add them: {{{1}}}. * The first and second numbers are still equal. So, the sum is in W.

Rule 2 (Multiplying by a Scalar):

* Take a point from W: {{{1}}}. * Take any number c. Multiply: {{{1}}}. * The first and second numbers are still equal. So, the result is in W. This shows W is a subspace.

Example III: Continuous Functions

Imagine all possible functions that map real numbers to real numbers. Let's call this big space V. Now, consider a smaller group of functions: all the continuous functions. These are functions you can draw without lifting your pencil. Let's call this set C(R).

Proof that C(R) is a subspace:

The zero function (f(x) = 0 for all x) is continuous. So, C(R) is not empty.
If you add two continuous functions, the result is always a continuous function. (This is a rule you learn in calculus.)
If you multiply a continuous function by any number, the result is also a continuous function.

So, C(R) is a subspace of all functions.

Example IV: Differentiable Functions

Similar to the last example, if you take the set of all differentiable functions (functions whose slope can be found at every point), this also forms a subspace. This is because adding differentiable functions gives a differentiable function, and multiplying a differentiable function by a number also gives a differentiable function.

How Subspaces Behave

Subspaces are always "closed" under addition and scalar multiplication. This means that if you start with vectors in a subspace and do these operations, you'll always stay within that subspace.

In simple terms, a set is a subspace if it's not empty and if any combination of its elements (like adding them or multiplying them by numbers) always stays within that set.

Describing Subspaces

There are several ways to describe subspaces:

Equations: A subspace can be defined by a set of linear equations where everything equals zero (called "homogeneous" equations). For example, z = 0 in Example I, or x = y (which can be written as x - y = 0) in Example II.
Spanning Vectors: A subspace can be built from a collection of vectors. This is called the linear span.
Geometric Shapes: In geometry, especially in 2D or 3D space, a subspace is like a flat shape (a line, a plane, etc.) that always passes through the origin (0,0,0).

Let's look closer at how we can describe them.

Using Systems of Linear Equations

Imagine you have a set of equations like this: 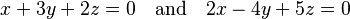$x + 3y + 2z = 0 \quad\text{and}\quad 2x - 4y + 5z = 0$ The set of all points (x, y, z) that solve both these equations forms a subspace. This subspace is a line in 3D space that passes through the origin.

The Null Space of a Matrix

When you have a system of linear equations, you can write it using a matrix. The set of all solutions to the equation (where A is a matrix and x is a vector) is called the null space of the matrix. This null space is always a subspace.

For example, the equations above can be written as: 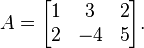$A = \begin{bmatrix} 1 & 3 & 2 \\ 2 & -4 & 5 \end{bmatrix} .$ The null space of this matrix A is the line we just talked about.

Building with Parametric Equations

You can also describe a subspace using parametric equations. This is like saying, "Every point in this subspace can be made by combining these basic parts."

For example, points (x, y, z) described by: 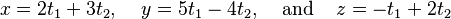$x = 2t_1 + 3t_2,\;\;\;\;y = 5t_1 - 4t_2,\;\;\;\;\text{and}\;\;\;\;z = -t_1 + 2t_2$ form a two-dimensional subspace (a plane) in 3D space. Here, t₁ and t₂ are just numbers that can be anything.

Spanning Vectors

The idea of parametric equations leads to spanning vectors. In the example above, the points are made by combining two special vectors: (2, 5, -1) and (3, -4, 2). 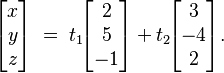$\begin{bmatrix} x \\ y \\ z \end{bmatrix} \;=\; t_1 \!\begin{bmatrix} 2 \\ 5 \\ -1 \end{bmatrix} + t_2 \!\begin{bmatrix} 3 \\ -4 \\ 2 \end{bmatrix}.$ This is called a linear combination of these two vectors.

The set of all possible linear combinations of a group of vectors is called their span. The span of any set of vectors is always a subspace. 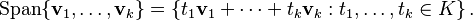$\text{Span} \{ \mathbf{v}_1, \ldots, \mathbf{v}_k \} = \left\{ t_1 \mathbf{v}_1 + \cdots + t_k \mathbf{v}_k : t_1,\ldots,t_k\in K \right\} .$ Geometrically, the span is the "flat" shape (line, plane, etc.) that goes through the origin and includes all the given vectors.

Example

The xz-plane

The xz-plane in 3D space (where y is always 0) can be described by:

x = t_1, \;\;\; y = 0, \;\;\; z = t_2.

This plane is spanned by the vectors (1, 0, 0) and (0, 0, 1). Any point on the xz-plane can be written as:

(t_1, 0, t_2) = t_1(1,0,0) + t_2(0,0,1)\text{.}

This means you can reach any point on that plane by moving some distance along the x-axis (using (1,0,0)) and then some distance along the z-axis (using (0,0,1)).

Column Space and Row Space

When you have a matrix, its column space is the subspace spanned by its column vectors. Similarly, its row space is the subspace spanned by its row vectors. These are important in understanding how matrices work.

Independence, Basis, and Dimension

The vectors u and v are a basis for this two-dimensional subspace of R³. They are independent and can create any point on the plane.

Sometimes, you might have many vectors that span a subspace, but some of them might be "redundant." Vectors are linearly independent if none of them can be created by combining the others. If vectors are independent, then each point in their span has a unique way of being formed by those vectors.

A basis for a subspace S is a set of linearly independent vectors that together span the entire subspace S. The number of vectors in a basis tells you the dimension of the subspace. For example, a line has dimension 1, a plane has dimension 2, and our 3D space has dimension 3.

Example

A 2D plane in 4D space

Let S be a subspace in 4D space (R⁴) defined by the equations:

x_1 = 2 x_2\;\;\;\;\text{and}\;\;\;\;x_3 = 5x_4.

The vectors (2, 1, 0, 0) and (0, 0, 5, 1) form a basis for S. This means any point in S can be uniquely written as:

(2t_1, t_1, 5t_2, t_2) = t_1(2, 1, 0, 0) + t_2(0, 0, 5, 1).

This subspace S is two-dimensional, even though it lives in a 4D world!

Operations with Subspaces

Inclusion

One subspace can be "inside" another. For example, a line through the origin is "included" in a plane through the origin. If two subspaces have the same dimension and one is inside the other, then they must be the exact same subspace.

Intersection

In 3D space, when two different planes (two-dimensional subspaces) cross, their intersection is a line (one-dimensional).

If you have two subspaces, U and W, their intersection (written as U ∩ W) is the set of all vectors that are in both U and W. This intersection is always another subspace.

Proof that U ∩ W is a subspace:

Rule 1 (Adding Vectors): If you take two vectors that are in both U and W, then their sum will also be in U (because U is a subspace) and in W (because W is a subspace). So, their sum is in the intersection.
Rule 2 (Multiplying by a Scalar): If you take a vector that is in both U and W, and multiply it by a number, the result will be in U and in W. So, the result is in the intersection.
The zero vector is always in any subspace, so it's in both U and W, and thus in their intersection.

Sum

If U and W are subspaces, their sum (written as U + W) is the set of all vectors you can get by adding a vector from U and a vector from W. This sum is also a subspace.

For example, if you have two different lines through the origin in 3D space, their sum will be the plane that contains both lines.

The dimension of the sum is related to the dimensions of the original subspaces and their intersection by this formula: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \dim(U+W) = \dim(U) + \dim(W) - \dim(U \cap W).

If the only vector common to U and W is the zero vector (meaning their intersection is just {0}), then their sum is called a direct sum, written as 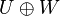$U \oplus W$ . In this case, the dimension of the direct sum is simply the sum of their individual dimensions: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \dim (U \oplus W) = \dim (U) + \dim (W)

How Computers Work with Subspaces

Many computer methods for dealing with subspaces use a process called row reduction. This is a way to simplify a matrix by applying certain operations to its rows. Row reduction helps us find important information about subspaces:

It doesn't change the null space (the set of solutions to Ax = 0).
It doesn't change the row space (the span of the row vectors).
It helps us see how the column vectors are related.

Finding a Basis for a Row Space

To find a basis for the row space of a matrix A:

Use row reduction to change A into a simpler form called row echelon form.
The rows that are not all zeros in this simpler form will be a basis for the row space of A.

Checking Subspace Membership

To check if a vector v is part of a subspace S (given its basis vectors {b₁, ..., b_k}):

Create a matrix where the rows are the basis vectors and the vector v.
Use row reduction on this matrix.
If the simplified matrix has a row of all zeros, then v is in the subspace S.

Finding a Basis for a Column Space

To find a basis for the column space of a matrix A:

Use row reduction to change A into row echelon form.
Look at the columns in the simplified matrix that have "pivots" (the first non-zero number in a row).
The original columns from A that correspond to these pivot columns form a basis for the column space.

Finding Coordinates for a Vector

If you know a vector v is in a subspace S and you have a basis {b₁, ..., b_k} for S, you can find the "coordinates" (numbers t₁, ..., t_k) that show how to combine the basis vectors to get v.

Create a matrix with the basis vectors as columns and v as the last column.
Use row reduction to simplify this matrix.
The numbers in the last column of the simplified matrix will be your coordinates.

Finding a Basis for a Null Space

To find a basis for the null space of a matrix A:

Use row reduction to put A into reduced row echelon form.
From this form, figure out which variables are "free" (can be any value) and which are "dependent" (their values depend on the free variables).
For each free variable, create a special vector by setting that free variable to 1 and all other free variables to 0. These special vectors form a basis for the null space.

Finding Equations for a Subspace

If you have a basis for a subspace S, you can find the equations that describe it:

Create a matrix with the basis vectors as rows.
Use row reduction to put this matrix into reduced row echelon form.
For each column without a pivot, write an equation that shows how that column relates to the pivot columns. These equations will describe the subspace.

Images for kids

One-dimensional subspaces in the two-dimensional vector space over the finite field F₅. The origin (0, 0), marked with green circles, belongs to any of six 1-subspaces, while each of 24 remaining points belongs to exactly one; a property which holds for 1-subspaces over any field and in all dimensions. All F₅² (i.e. a 5 × 5 square) is pictured four times for a better visualization

All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:

Linear subspace Facts for Kids. Kiddle Encyclopedia.