Logical consequence facts for kids

Logical consequence is a super important idea in logic. It helps us understand how different statements are connected.

Think of it like this: if one statement logically follows from another, then it's a logical consequence.

For example, in a valid logical argument, the conclusion is a logical consequence of the premises. This means the conclusion must be true if the premises are true.

Logicians study what it means for a conclusion to follow from premises. They also look at what makes something a logical truth.

Logical consequence is always true and follows a set pattern. It's like a rule that always works. A sentence is a logical consequence of other sentences if it has to be true when those other sentences are true. This is true no matter what you personally think about the sentences.

A logician named Alfred Tarski said that logical consequence has three main features:

• It depends on the logical form (the structure) of the sentences.
• You can figure it out without needing to do experiments or observe things (it's a priori).
• It involves ideas of what is necessary or possible.

What is formal logic?

The most common way to understand logical consequence is through formality. This means we look at the structure of statements, not what they are actually about.

Whether statements logically follow each other depends on their logical form. It does not depend on the specific words or ideas inside the statements.

How rules of inference work

Rules of inference use patterns or schemes. These patterns show how arguments are built. For example, here is a common logical pattern:

• All X are Y
• All Y are Z
• Therefore, all X are Z.

This argument is valid because its structure always works. Any time you put different things in for X, Y, and Z, if the first two statements are true, the last one must also be true.

Let's compare this to another example: "Fred is Mike's brother's son. Therefore Fred is Mike's nephew." This argument depends on the meanings of words like "brother," "son," and "nephew." It's not a formal consequence because its truth relies on the specific meanings of those words, not just the structure. A formal consequence works in all cases based only on its structure.

What is a priori knowledge?

If you know that statement Q logically follows from statement P, then nothing else you learn about P or Q will change that knowledge.

Our understanding that Q is a logical consequence of P does not come from experience. Arguments that are logically valid can be known without needing to observe the world. This means they are a priori.

Proofs and models in logic

There are two main ways to explain logical consequence: using proofs and using models.

• Studying logical consequence through proofs is called proof theory.
• Studying it through models is called model theory.

Syntactic consequence (proofs)

A statement A is a syntactic consequence of a set of statements (let's call it Gamma) within a formal system. This means you can create a formal proof of A starting from Gamma.

We write this as 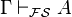. The symbol 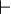(called a turnstile) was first used in 1879.

Syntactic consequence does not depend on how you interpret the formal system. It only cares about the rules of the system itself.

Semantic consequence (models)

A statement A is a semantic consequence of a set of statements (Gamma) within a formal system if there is no way for all statements in Gamma to be true while A is false.

We write this as .

In simpler words, if all statements in Gamma are true, then A must also be true. The situations where Gamma is true are always situations where A is also true.

What are modal accounts?

Modal accounts of logical consequence use ideas like necessary and impossible.

The main idea is:

• A is a logical consequence of Gamma if it is necessary that if all statements in Gamma are true, then A is also true.

Another way to say this is:

• A is a logical consequence of Gamma if it is impossible for all statements in Gamma to be true and A to be false.

These accounts are called "modal" because they use ideas of logical necessity and logical possibility. "It is necessary that" often means "it is true in all possible worlds."

So, the idea becomes:

• A is a logical consequence of Gamma if there is no possible world where all statements in Gamma are true and A is false.

Let's use an example:

• All frogs are green.
• Kermit is a frog.
• Therefore, Kermit is green.

The conclusion ("Kermit is green") is a logical consequence of the premises. Why? Because we cannot imagine any possible world where:

• All frogs are green (premise 1 is true)
• Kermit is a frog (premise 2 is true)
• But Kermit is NOT green (conclusion is false)

Combining modal and formal ideas

Some accounts combine modal and formal ideas. They say:

• A is a logical consequence of Gamma if it is impossible for an argument with the same logical form as Gamma/A to have true premises and a false conclusion.

Other ways to think about consequence

Warrant-based accounts

Most ideas about logical consequence focus on truth. They assume a good argument never goes from true statements to a false one.

However, some people suggest "warrant-preservational" accounts. These say that a good argument never goes from statements you can justifiably assert to a conclusion you cannot justifiably assert. This idea is favored by intuitionists.

Non-monotonic logical consequence

The ideas discussed so far usually lead to monotonic consequence relations. This means if A is a consequence of Gamma, then A is also a consequence of any larger set of statements that includes Gamma.

But sometimes, adding more information can change the consequence. This is called non-monotonic consequence. For example:

• "Birds can typically fly, Tweety is a bird."
• From this, you might conclude: "Tweety can fly."

However, if you add more information:

• "Birds can typically fly, Tweety is a bird, Tweety is a penguin."
• Now, you would NOT conclude: "Tweety can fly," because penguins don't fly.

See also