Formal system facts for kids
A formal system is like a special set of rules and symbols used in mathematics and logic. It helps us build new true statements, called theorems, from basic starting points, called axioms. Think of it as a very strict game with clear rules for what you can do.
In 1921, a famous mathematician named David Hilbert thought formal systems could be the strong foundation for all knowledge in mathematics. The word "formalism" can sometimes mean the same as "formal system." It can also refer to a specific way of writing things, like how Paul Dirac wrote down his physics equations.
Contents
What are Formal Systems?
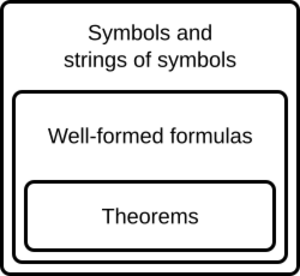
A formal system has two main parts:
- Formal language: This is like the alphabet and grammar of the system. It tells you how to make proper "sentences" (called well-formed formulas) using specific symbols.
- Deductive system: These are the rules that let you prove new things. You start with basic truths (the axioms) and use rules of inference to figure out more truths, which are the theorems. Both axioms and theorems are part of the formal language.
Formal Language
A formal language is a language defined by a formal system. Just like regular languages we speak, formal languages have two sides:
- Syntax: This is about how the language looks. It's the set of all possible expressions that are correct in that language.
- Semantics: This is about what the expressions in the language actually mean.
Usually, when we talk about a formal language, we mostly focus on its syntax. This is done using a formal grammar. There are two main types of formal grammar:
- Generative grammars give rules for how to write strings (sequences of symbols) in the language.
- Analytic grammars give rules for how to check if a string belongs to the language.
Deductive System
A deductive system is also called a deductive apparatus. It includes the axioms (basic truths) and the rules of inference. These rules are used to derive (figure out) the theorems of the system.
These systems help us keep track of true statements. Usually, we care about whether a statement is true or false. But other ideas, like whether something is "justified" or "believed," can also be preserved.
For a deductive system to work correctly, its rules must be clear. They should not depend on what the language is supposed to mean. The goal is to make sure each step in a proof comes directly from the steps before it.
An example of a deductive system is the rules and axioms about "equality" used in first-order logic.
There are two main ways to think about deductive systems:
- Proof systems
- Formal semantics
Proof System
Formal proofs are like a step-by-step recipe. They are sequences of well-formed formulas (WFFs). Each WFF is either an axiom or comes from applying a rule to earlier WFFs. The very last WFF in the sequence is the theorem that has been proven.
Once a formal system is set up, we can define all the theorems that can be proven within it. All axioms are considered theorems. It's not always easy to tell if a given WFF is a theorem or not.
The idea that mathematics is all about creating formal proofs is called formalism. David Hilbert started a field called metamathematics. This field studies formal systems themselves. Any language we use to talk about a formal system is called a metalanguage. The formal system we are studying is called the object language.
Formal Semantics
A logical system combines a deductive system with extra basic truths (non-logical axioms). In model theory, a logical system can be given different interpretations. These interpretations describe whether a specific way of understanding the symbols (a structure) makes a well-formed formula true. A structure that makes all the axioms of the system true is called a model.
A logical system is:
- Sound: If every formula that can be proven from the axioms is true in every model of the system.
- Semantically complete: If every formula that is true in every model of the system can be proven from the axioms.
An example of a logical system is Peano arithmetic. This system describes the rules for numbers. Its standard model uses the nonnegative integers (0, 1, 2, 3...) and gives the symbols their usual meaning.
History of Formal Systems
Early logic systems came from different parts of the world. These include Indian logic by Pāṇini, the logic of Aristotle, and Chinese logic by Gongsun Long. Later, people like George Boole, Augustus De Morgan, and Gottlob Frege made important contributions. Mathematical logic really grew in 19th-century Europe.
David Hilbert started a movement called Hilbert's program. He wanted to solve problems in the foundations of mathematics by using formal systems. However, Gödel's incompleteness theorems later showed that there were limits to what formal systems could do.
See also
- List of formal systems
- Formal method
- Formal science
- Logic translation
- Rewriting system
- Substitution instance
- Theory (mathematical logic)

