Mersenne prime facts for kids

A Mersenne number is a special kind of number in mathematics. It's a number that is one less than a power of two.

We can write a Mersenne number using this formula: M_n = 2ⁿ − 1.

A Mersenne prime is a Mersenne number that is also a prime number. For a Mersenne number to be a Mersenne prime, the exponent n in the formula 2ⁿ − 1 must also be a prime number.

For example, the number 31 is a Mersenne number because it can be written as 2⁵ − 1. Here, the exponent '5' is a prime number. Since 31 itself is also a prime number, 31 is a Mersenne prime.

However, not all Mersenne numbers are prime. For instance, 2047 is a Mersenne number (2¹¹ − 1), but it's not a prime number because you can divide it by 23 and 89. Also, 15 (which is 2⁴ − 1) is not a Mersenne prime because its exponent '4' is not a prime number.

Why Mersenne Primes Are Important

For a long time, the biggest prime numbers ever found have usually been Mersenne primes. This is because there are special math tricks and computer programs that make it easier to find very large Mersenne primes compared to other types of prime numbers.

Mersenne Primes and Perfect Numbers

Mersenne primes have a cool connection to something called perfect numbers. A perfect number is a number that is equal to the sum of its "proper divisors" (all the numbers that divide into it evenly, except for itself). For example, the proper divisors of 6 are 1, 2, and 3. If you add them up (1 + 2 + 3), you get 6! So, 6 is a perfect number.

Long ago, in the 4th century BC, a famous Greek mathematician named Euclid discovered something amazing. He showed that if you have a Mersenne prime (let's call it M), then the number you get from the formula M(M+1)/2 will always be a perfect number.

Much later, in the 18th century, another brilliant mathematician named Leonhard Euler proved that all even perfect numbers can be found using Euclid's formula with a Mersenne prime. We don't know if any odd perfect numbers exist, but mathematicians suspect there aren't any. If an odd perfect number did exist, it would have to be incredibly huge!

How Many Mersenne Primes Are There?

Mathematicians are still trying to figure out if there are an endless number of Mersenne primes. Most experts who study this topic believe there are. Some mathematicians have even developed formulas to guess how many Mersenne primes might exist up to a certain number.

Mersenne Numbers in Binary

The binary (base-2) way of writing a Mersenne number (2ⁿ - 1) is very simple. It's just the digit '1' repeated n times.

For example, 2⁵ - 1 equals 31 in our normal number system. In binary, 31 is written as 11111, which is the digit '1' repeated 5 times.

History of Mersenne Primes

The first four Mersenne primes were known by the Ancient Greeks. These are 3, 7, 31, and 127. The next one, 8191, was discovered much later in 1456.

People have always been fascinated by finding big prime numbers. Because of the special properties of Mersenne primes, and the clever ways we can test them, the largest known prime numbers today are almost always Mersenne primes.

As of December 21, 2018, 51 Mersenne primes have been found. The largest known prime number is a Mersenne prime: 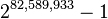. This number is so big, it has over 24 million digits!

See also

In Spanish: Número primo de Mersenne para niños