Parity (mathematics) facts for kids
In mathematics, parity is a special quality of a whole number (an integer) that tells us if it is even or odd. An integer is called even if you can divide it by two with no remainder. If you can't divide it by two evenly, then it's an odd number.
For example, numbers like -4, 0, and 82 are even. This is because you can multiply another whole number by 2 to get them:
- -2 multiplied by 2 equals -4
- 0 multiplied by 2 equals 0
- 41 multiplied by 2 equals 82
On the other hand, numbers like -3, 5, 7, and 21 are odd. The idea of parity (even or odd) only applies to whole numbers. It doesn't apply to numbers like 1/2 or 4.201.
Even and odd numbers have opposite parities. For example, 22 is an even number, and 13 is an odd number. They have different parities. The number zero (0) is always considered an even number. Any two whole numbers that are right next to each other (like 5 and 6) will always have opposite parities.
When you look at a number written in the decimal system (our usual number system), you can tell if it's even or odd by its very last digit.
- If the last digit is 1, 3, 5, 7, or 9, the number is odd.
- If the last digit is 0, 2, 4, 6, or 8, the number is even.
This trick works for any number system that uses an even base, like the binary numeral system (base 2). In binary, a number is odd if its last digit is 1, and even if its last digit is 0.
Contents
What Are Even and Odd Numbers?
An even number is any integer that can be written as: 
Here, k is any whole number (positive, negative, or zero). This means an even number is simply a multiple of 2.
An odd number is any integer that can be written as: 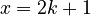Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle x = 2k + 1} Again, k is any whole number. This means an odd number is always one more than an even number.
Another way to think about it is that an even number can be divisible by 2 without any remainder. An odd number cannot be divided by 2 evenly.
How Even and Odd Numbers Work Together
The rules for adding, subtracting, and multiplying even and odd numbers are simple. They are often used to quickly check if a math problem's answer might be correct.
Adding and Subtracting Parity
- Even + Even = Even (Example: 2 + 4 = 6)
- Even + Odd = Odd (Example: 2 + 3 = 5)
- Odd + Odd = Even (Example: 3 + 5 = 8)
The same rules apply for subtraction:
- Even - Even = Even (Example: 6 - 2 = 4)
- Even - Odd = Odd (Example: 6 - 3 = 3)
- Odd - Odd = Even (Example: 5 - 3 = 2)
Multiplying Parity
- Even × Even = Even (Example: 2 × 4 = 8)
- Even × Odd = Even (Example: 2 × 3 = 6)
- Odd × Odd = Odd (Example: 3 × 5 = 15)
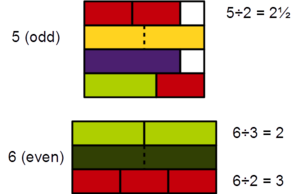
Dividing Parity
When you divide two whole numbers, the answer isn't always a whole number. For example, 1 divided by 4 is 1/4, which is neither even nor odd. The ideas of even and odd only apply to whole numbers.
However, if the result of a division is a whole number, it will be even if the top number (dividend) has more factors of two than the bottom number (divisor).
A Little Bit of History
Long ago, the ancient Greeks had different ideas about numbers. Some of them thought that the number 1 was special. They believed it was neither fully odd nor fully even. This idea stuck around for a long time. Even in the 1800s, a teacher named Friedrich Fröbel taught his students that 1 was neither even nor odd. He thought it was like a balancing point between the two.
Parity in Higher Math and Games
Parity shows up in many interesting ways beyond just simple numbers.
Parity in Chess and Grids
Imagine a grid, like a chessboard. Each square can be given a "parity" based on its position. This is usually done by adding up the coordinates of the square. For example, if a square is at (1,1), the sum is 2 (even). If it's at (1,2), the sum is 3 (odd).
In chess, the color of a square shows its parity.
- Bishops always stay on squares of the same color (same parity).
- Knights always jump from a square of one color to a square of the opposite color (they change parity with each move).
This idea helped solve a famous puzzle called the mutilated chessboard problem. If you remove two opposite corner squares from a chessboard, you can't cover the rest of the board with dominoes. This is because each domino covers one white square and one black square. But when you remove opposite corners, you're left with two more squares of one color than the other, making it impossible to cover evenly.
Parity and Prime Numbers
All prime numbers (numbers only divisible by 1 and themselves) are odd, except for one special prime number: 2. The number 2 is the only even prime number.
Scientists are still trying to prove Goldbach's conjecture. This idea says that every even number greater than 2 can be made by adding two prime numbers together. For example, 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5. Computers have checked this for very, very large numbers, but there's no full mathematical proof yet!
Parity in Puzzles
In puzzles like the Rubik's Cube, the idea of parity is very important. When you twist the cube, you are performing "permutations" (swapping pieces around). Each move on a Rubik's Cube results in an "even permutation" of the pieces. This means that you can't just swap two pieces without affecting others in a way that keeps the overall "evenness" of the puzzle. Understanding parity helps puzzle solvers know which moves are possible and which are not.
Evil and Odious Numbers
In some math games, numbers are called "evil" or "odious" based on their binary form.
- An evil number has an even number of 1s in its binary representation (like 3 is 11 in binary, two 1s, so it's evil).
- An odious number has an odd number of 1s in its binary representation (like 5 is 101 in binary, two 1s, so it's odious).
These numbers are important in the strategy for games like Kayles.
Everyday Uses of Parity
Parity isn't just for math class; it's used in many practical ways!
Error Detection
In computers and data transfer, a parity bit is a simple way to check for errors. When information is sent, an extra bit (a 0 or 1) is added to a binary number. This bit makes the total number of 1s either even or odd, depending on the system. If even one bit gets changed during transmission, the parity will be wrong, and the computer knows there was an error. This helps detect mistakes in data.
Music Instruments
Some musical instruments, like a clarinet, have a cylindrical shape and are closed at one end. When you play them, the sounds they make (called harmonics) are only odd multiples of the main note. This is why a clarinet sounds different from a flute, which produces both even and odd harmonics.
Numbering Systems
You might have noticed that on many streets, houses on one side have even numbers, and houses on the other side have odd numbers. This makes it easier to find addresses.
Similarly, in the United States numbered highways, even numbers usually mean the highway goes east-west, while odd numbers mean it goes north-south. For airline flight numbers, even numbers often mean the flight is going east or north, and odd numbers mean it's going west or south.
See also
In Spanish: Números pares e impares para niños
- Divisor
- Half-integer
