Philosophical logic facts for kids

Philosophical logic is a part of logic that looks at how we can use logical tools to solve problems in philosophy. It often involves creating new kinds of logical systems, like modal logic.

Imagine logic as a set of rules for good thinking and arguing. Classical logic is the most common set of these rules. It helps us figure out if an inference (a step in reasoning from facts to a conclusion) is correct. For example, if you know "All cats like fish" and "Whiskers is a cat," classical logic helps you conclude "Whiskers likes fish."

But sometimes, classical logic isn't enough. Philosophical logic explores two main ways to go beyond it:

• Extended logics add new ideas to classical logic. They keep the old rules but introduce new symbols and rules to talk about things like what is possible, what we should do, or what is known.
• Deviant logics challenge some of the basic rules of classical logic. They offer different ways of thinking about truth or how arguments work.

Philosophical logic helps us understand deep philosophical ideas in a very precise way.

What is Logic?

Logic is the study of valid inferences. An inference is when you move from some starting ideas (called premises) to a new idea (called a conclusion). Think of it like a detective using clues to figure out what happened.

An inference is valid if the conclusion must be true whenever the premises are true. It's impossible for the premises to be true and the conclusion false. Logic helps us find the rules that make an inference valid.

Classical logic is the most common type of logic. It uses rules that many people naturally agree with, like the idea that something is either true or false (the law of excluded middle). But philosophical logic also looks at other ways to define valid thinking.

Types of Logic

Over time, many different logical systems have been created. We can group them into two main types:

Extended Logics

Extended logics are like adding new features to classical logic. They accept the basic rules of classical logic but then expand them to cover new areas. They do this by adding new symbols and rules for those symbols.

Logic of Possibility and Necessity

Alethic modal logic helps us talk about what is possible or necessary. Classical logic only deals with what is simply true.

• We use a special symbol (like a diamond ) for possible. So, " it rains" means "it is possible that it rains."
• We use another symbol (like a box ) for necessary. So, " it rains" means "it is necessary that it rains."

This logic often uses the idea of possible worlds. A possible world is just a way things could have been.

• Something is possibly true if it's true in at least one possible world.
• Something is necessarily true if it's true in all possible worlds.

Logic of Right and Wrong

Deontic logic applies logic to ethics, which is about right and wrong. It helps us understand ideas like obligation (what we must do) and permission (what we are allowed to do).

• We use a symbol (like 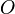) for obligation. So, " 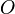you help" means "you have an obligation to help."
• We use another symbol (like 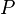) for permission. So, " 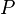you help" means "you have permission to help."

These symbols behave logically similar to "necessary" and "possible." For example, if you must do something, you are also allowed to do it.

Logic of Time

Temporal logic (or tense logic) uses logic to talk about time. It has symbols to show if something was true in the past, is true now, or will be true in the future.

• For example, one symbol might mean "it was the case that..."
• Another might mean "it will be the case that..."

This helps us make precise statements about when things happen. For instance, "It will always be rainy in London" can be written with a special symbol. From this, we can logically conclude "It will be rainy in London at some time."

Logic of Knowledge and Belief

Epistemic logic is about the logic of knowledge and belief. It uses symbols to express what someone knows or believes.

• A symbol (like 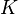) can mean "the agent knows that..."
• Another symbol (like 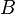) can mean "the agent believes that..."

For example, if "Socrates is wise" is true, then "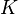 Socrates is wise" means "the agent knows that Socrates is wise." One important rule in this logic is that if you know something, it must be true. You can't "know" something that's false.

Higher-Order Logic

Higher-order logics are more powerful than classical logic. Classical logic can only talk about individual things (like "all cats"). Higher-order logic can also talk about properties or qualities of things.

• For example, classical logic can say "There are some apples that are sweet."
• Higher-order logic can say "There are some qualities that Mary and John share" (like being tall or being kind).

This makes higher-order logic very useful for expressing complex ideas, especially in mathematics. However, it's also more complex and not as widely used as classical logic.

Deviant Logics

Deviant logics are different from extended logics because they change some of the basic rules of classical logic. They are often seen as rivals to classical logic.

Intuitionistic Logic

Intuitionistic logic is a stricter version of classical logic. It rejects some common rules, like the law of excluded middle (which says something is either true or false).

• This logic is based on the idea that something is true only if we can prove it.
• So, if we can't prove that "A" is true, and we can't prove that "not A" is true, then the law of excluded middle doesn't apply.

This logic was first used in mathematics. It suggests that mathematical objects only exist if we can mentally construct them.

Free Logic

Free logic deals with names or descriptions that don't refer to anything real, like "Santa Claus" or "Pegasus." In classical logic, every name must refer to something that exists.

• Free logic allows statements like "Santa Claus does not exist" to be true, even though "Santa Claus" doesn't refer to a real person.
• This means some rules of classical logic don't work in free logic. For example, from "Santa Claus has a beard," you can't automatically conclude "Something has a beard" in free logic.

This logic helps us talk about fictional characters or things that don't exist without causing logical problems.

Many-Valued Logics

Many-valued logics challenge the idea that something can only be true or false. They allow for more than two truth values.

• The simplest versions are three-valued logics, which might have "true," "false," and "undefined."
• Some logics even have four truth values, like "true," "false," "neither true nor false," and "both true and false."
• Fuzzy logic is an extreme example. It says truth can be any degree between 0 (completely false) and 1 (completely true). This is useful for vague ideas, like how "young" someone is. A 3-year-old is "more true" to being young than a 23-year-old.

Paraconsistent Logics

Paraconsistent logics are special because they can handle contradictions without everything falling apart. In classical logic, if you have a contradiction (like "A is true" and "A is false"), you can logically prove anything from it. This is called the principle of explosion.

• Paraconsistent logics change their rules so that a contradiction doesn't make the whole system meaningless.
• This is important for people who believe that reality itself might have contradictions, or for studying group beliefs where different people might hold conflicting ideas.

Relevance Logic

Relevance logic is a type of paraconsistent logic. Its main goal is to fix a problem with how classical logic handles "if-then" statements.

• In classical logic, "if all lemons are red then there is a sandstorm inside the Sydney Opera House" is considered true, even though lemons and sandstorms have nothing to do with each other.
• Relevance logic says that for an "if-then" statement to be true, the "if" part must be relevant to the "then" part. This makes logic closer to how we think in everyday language.