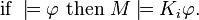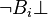Epistemic modal logic facts for kids
Epistemic modal logic is a special part of modal logic that helps us think about knowledge. While people have thought about knowledge since Ancient Greece, epistemic logic is quite new. It's used in many areas like philosophy, theoretical computer science, artificial intelligence, economics, and linguistics.
Thinkers like Aristotle and later medieval philosophers talked about modal logic. But it was C. I. Lewis who first made a clear, symbolic system for it in 1912. The field became what it is today in 1963, thanks to the work of Kripke.
Contents
How Epistemic Logic Grew
Many papers in the 1950s mentioned a logic for knowledge. But the paper An Essay in Modal Logic by G. H. von Wright in 1951 is seen as the start.
Then, in 1962, another Finnish thinker, Hintikka, wrote Knowledge and Belief. This was the first book to suggest using "modalities" (like "it is known that") to understand knowledge. Before this, modalities were mostly used for things that are "necessary" or "possible."
Since then, a lot more research has happened. For example, epistemic logic has joined with dynamic logic. This new field, called dynamic epistemic logic, helps us understand how information changes. It also shows how people share information in systems with many different "agents" (like computer programs or people).
Thinking About Knowledge with Possible Worlds
Most ways of understanding knowledge use the idea of "possible worlds." Imagine all the different ways the world could be. When you know something, you rule out some of these possible worlds.
For example, if you know it's either Friday or Saturday, you know it's not Thursday. This means there are no possible worlds where it's Thursday that are still "possible" for you, given what you know. In all the worlds you consider possible, it's either Friday or Saturday.
There are two main ways to use this idea:
- Logic-based approach: This uses Kripke semantics. It's like building a map of possible worlds and how they connect.
- Event-based approach: This uses set theory and sees "events" as groups of possible worlds.
The logic-based way is often used in philosophy and AI. The event-based way is more common in game theory and mathematical economics. We will focus on the logic-based approach here.
What the Symbols Mean
The main symbol in epistemic logic is K. It means "it is known that." If there's more than one person or "agent," we add a small number. So, 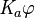 means "Agent
means "Agent 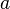 knows that
knows that  is true."
is true."
This makes epistemic logic a type of multimodal logic. It's used for knowledge representation in computers.
What if someone *doesn't* know something? We can write 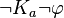 . This means "Agent
. This means "Agent 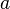 doesn't know that
doesn't know that  is false." Or, "It's possible, given what
is false." Or, "It's possible, given what 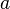 knows, that
knows, that  is true."
is true."
If agent 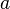 doesn't know if
doesn't know if  is true or false, we write
is true or false, we write 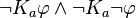 .
.
We can also add symbols for group knowledge:
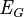 : "Every agent in group G knows." (This is mutual knowledge).
: "Every agent in group G knows." (This is mutual knowledge).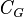 : "It is common knowledge to every agent in G."
: "It is common knowledge to every agent in G."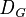 : "It is distributed knowledge to the whole group G."
: "It is distributed knowledge to the whole group G."
How the Symbols Work (Semantics)
The logic-based approach uses Kripke structures (also called Kripke models). Imagine a Kripke structure as a map. This map has:
- A set of states or possible worlds (like different scenarios).
- A way to tell if a statement is true or false in each state.
- Binary relations (
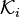 ) for each agent. These show which states an agent considers "possible" from their current state.
) for each agent. These show which states an agent considers "possible" from their current state.
It's important not to mix up 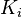 (the "knows that" symbol) and
(the "knows that" symbol) and 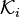 (the "possibility" connection between worlds).
(the "possibility" connection between worlds).
The "truth assignment" tells us if a statement 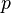 is true in a certain state
is true in a certain state  . So,
. So, 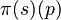 means
means 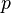 is true in state
is true in state  . Something true in one world might not be true in another.
. Something true in one world might not be true in another.
We write 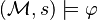 to say that statement
to say that statement  is true in state
is true in state  within model
within model 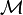 .
.
The 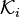 relation shows what worlds agent i thinks are possible. If
relation shows what worlds agent i thinks are possible. If 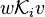 , it means agent i thinks world v could be the real world, given what they know in world w. These are called "epistemic alternatives."
, it means agent i thinks world v could be the real world, given what they know in world w. These are called "epistemic alternatives."
For an ideal idea of knowledge (like a perfect thinker), 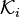 is usually an equivalence relation. This means it's:
is usually an equivalence relation. This means it's:
- Reflexive: You consider your current world possible.
- Symmetric: If you think world A is possible from world B, then world B is possible from world A.
- Transitive: If you think world A is possible from B, and B is possible from C, then A is possible from C.
These qualities make sense for knowledge, but not always for belief.
What Knowledge Is Like (S5 Properties)
If we assume 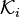 is an equivalence relation and agents are perfect thinkers, we can find some rules about knowledge. These are often called the "S5 Properties."
is an equivalence relation and agents are perfect thinkers, we can find some rules about knowledge. These are often called the "S5 Properties."
The Distribution Axiom (K)
This rule says that if an agent knows  and also knows that "if
and also knows that "if  is true, then
is true, then 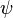 is true," then the agent must also know
is true," then the agent must also know 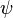 .
.
This is like saying if you know A, and you know A leads to B, then you know B.
The Knowledge Generalization Rule (N)
This rule says that if a statement  is always true (a tautology), then an agent knows it. This doesn't mean if
is always true (a tautology), then an agent knows it. This doesn't mean if  is true, you automatically know it. It means if
is true, you automatically know it. It means if  is true in *every* possible world an agent considers, then the agent must know
is true in *every* possible world an agent considers, then the agent must know  .
.
The Knowledge or Truth Axiom (T)
This rule, also called T, says that if an agent knows something, it must be true. You can believe something false, but you can't *know* something false.
This means if you know it, it's true.
The Positive Introspection Axiom (4)
This rule says that agents "know that they know what they know." If you know something, you know that you know it.
Some people, like Timothy Williamson, argue against this rule.
The Negative Introspection Axiom (5)
This rule says that agents "know that they don't know what they don't know." If you don't know something, you know that you don't know it.
Axiom Systems
Different groups of these rules create different "modal logics." The logic that uses K, T, 4, 5, and the Knowledge Generalization Rule is called S5. That's why the rules above are called S5 Properties.
Epistemic logic also looks at belief. For belief, we use B instead of K. The "truth axiom" (T) doesn't work for belief, because you can believe something that isn't true. Instead, we use the Consistency Axiom, D:
This means an agent doesn't believe a contradiction (something that is always false). When D replaces T in S5, the system is called KD45. The logic of belief is called doxastic logic.
Multiple Agents
When there are many agents, like in a computer system, each agent i has its own knowledge operator 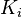 . We usually assume that each agent's way of thinking is common knowledge among all agents.
. We usually assume that each agent's way of thinking is common knowledge among all agents.
Challenges with the Possible World Model
One big problem with the possible worlds approach is "logical omniscience." This means that if an agent knows something, they automatically know *all* the things that logically follow from it.
For example, if you know the definition of a prime number, this logic says you instantly know if a huge, complex number is prime or not. This is because if the definition is true, and the number is prime, then it logically follows that the number is prime.
This shows that epistemic modal logic describes an ideal kind of knowledge, not how humans actually know things. Humans don't instantly know every logical consequence of what they know. If they did, there would be no unsolved math problems!
The Epistemic Fallacy (Masked-Man Fallacy)
The masked-man fallacy is a mistake in logic. It happens when you wrongly use the idea that if two things are identical, they must have all the same properties. This fallacy is "epistemic" because it mixes up what someone *knows* about an object with the object itself.
Examples of the Fallacy
The name comes from this example:
- Fact 1: I know who Bob is.
- Fact 2: I do not know who the masked man is.
- Conclusion: Therefore, Bob is not the masked man.
This conclusion might be wrong! Bob could be the masked man, and you just don't know it. Your knowledge (or lack of it) doesn't change who Bob is.
In symbols, it looks like this:
- Fact 1: The speaker believes they know who X is.
- Fact 2: The speaker believes they do not know who Y is.
- Conclusion: Therefore, the speaker believes X is not Y.
Another example:
- Fact 1: Lois Lane thinks Superman can fly.
- Fact 2: Lois Lane thinks Clark Kent cannot fly.
- Conclusion: Therefore, Superman and Clark Kent are not the same person.
Again, this conclusion is wrong. Lois Lane's beliefs don't change the fact that Superman and Clark Kent are the same person. The correct conclusion is that Lois Lane *believes* they are not the same person.
See also
 In Spanish: Lógica epistémica para niños
In Spanish: Lógica epistémica para niños
- Epistemic closure
- Epistemology
- Dynamic epistemic logic
- Logic in computer science
- Philosophical Explanations