Polar coordinate system facts for kids
In mathematics, the polar coordinate system is a way to find any point on a flat surface using two main pieces of information. Instead of using "x" and "y" like in a regular graph, it uses a distance from a central point and an angle from a starting line.
This system is super helpful when you're dealing with things that involve circles or rotations. For example, if you want to describe the path of a planet around the sun, polar coordinates can make it much simpler than using the usual "x" and "y" coordinates.
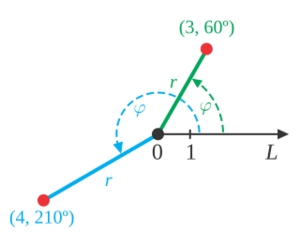
Every point in the polar system has two coordinates:
- The radial coordinate (usually called r) tells you how far the point is from the center. This center point is called the pole.
- The angular coordinate (often called θ or phi) tells you the angle from a special starting line. This line is called the polar axis. You measure this angle either clockwise or counter-clockwise from the polar axis.
Contents
History of Polar Coordinates
People have been using ideas like angles and distances for a very long time, even before the BCE. For example, Hipparchus (who lived from 190-120 BCE) made tables that used angles to figure out the positions of stars.
Later, a famous Greek mathematician named Archimedes described a special curve called the Archimedean spiral. For this spiral, the distance from the center changes depending on the angle. However, these early ideas weren't a full coordinate system like we have today.
The idea of a formal polar coordinate system came about in the mid-1600s. Two mathematicians, Grégoire de Saint-Vincent and Bonaventura Cavalieri, came up with similar ideas on their own. Cavalieri was one of the first to use polar coordinates to solve a problem about the area inside an Archimedean spiral. Another mathematician, Blaise Pascal, also used polar coordinates to measure the length of curves.
Sir Isaac Newton also looked at how to change between polar coordinates and other systems in his book Method of Fluxions (written in 1671). Later, in 1691, Jacob Bernoulli used a system with a "pole" and a "polar axis" to describe points by their distance from the pole and their angle from the axis.
The actual name "polar coordinates" was first used by Gregorio Fontana in the 1700s. It appeared in English in 1816. Later, Alexis Clairaut and Leonhard Euler helped develop the idea of using polar coordinates in three dimensions.
Changing Between Polar and Cartesian Coordinates
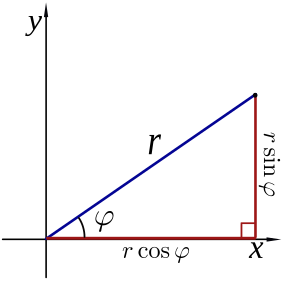
Sometimes you might need to switch between polar coordinates (r and φ) and the more common Cartesian coordinates (x and y).
To go from polar (r, φ) to Cartesian (x, y):
- x = r × cos(φ)
- y = r × sin(φ)
Here, "cos" and "sin" are trigonometric functions.
To go from Cartesian (x, y) to polar (r, φ):
- r = √(x² + y²) (This comes from the Pythagorean theorem, like finding the hypotenuse of a right triangle).
- φ can be found using the arctangent function, but it's a bit trickier because you need to consider which part of the graph the point is in.
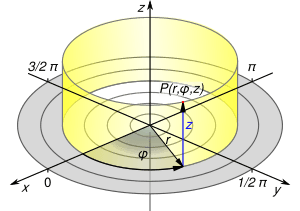
Cylindrical Coordinates
Cylindrical coordinates are like an upgrade from polar coordinates. They take the same idea of using a distance (r) and an angle (φ) on a flat surface, but they add a third dimension: height. This height is usually called Z.
So, to find a point in 3D space using cylindrical coordinates, you need:
- A distance r from the central axis.
- An angle φ around the axis.
- A height Z above or below the flat plane.
Imagine a point on the surface of a cylinder – that's where cylindrical coordinates are super useful!
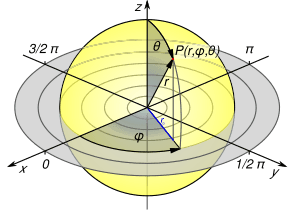
Spherical Coordinates
Spherical coordinates are another way to extend polar coordinates into three dimensions. Instead of using two distances and one angle, this system uses one distance and two angles.
To find a point in 3D space using spherical coordinates, you need:
- A distance r from the origin (the center of the sphere).
- An angle φ (phi), which is like the longitude on Earth.
- An angle θ (theta), which is like the latitude on Earth (but usually measured from the "north pole" down).
This system is perfect for describing points on the surface of a sphere, like locations on a globe or the position of stars in the sky.
Related pages
Images for kids
See also
 In Spanish: Coordenadas polares para niños
In Spanish: Coordenadas polares para niños